Team:iHKU/modeling
From 2008.igem.org
ModelingCONTENTS:
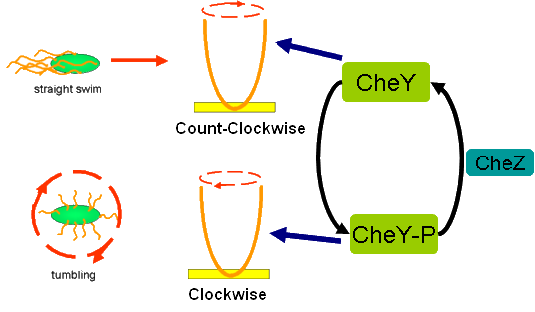
Cell Movement in Microscopic and Macroscopic AspectBasically, we considered the movement of a cell as a process of random walk, since an individual E.coli cell was always in the states between moving and tumbling (Fig.1).Similar to Brownian particles, the random walk of E.coli followed the Einstein-Smoluchowski theory [1].
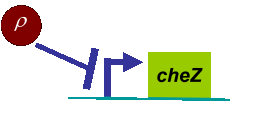
Fig . 1 Genetic circuit related to cell movementin(left) and cell random walk(right)
Firstly, for the one dimension of random walk, let x (t) denote the position of an E.coli cell at time t, given that its position coincided with the point x=0 at time t=0. And we assumed an E.coli cell moves an average distance l—in either the positive or negative direction of the x-axis—each step (during a time (τ) between two tumbling states). The probability that the cell was found at the point x at time t was now equal to the probability that, in a series of n (=t/τ) successive moving steps, the cell made m more steps in the positive direction of the axis than in the negative direction. The desired probability was given by the binomial expression [1, 2] 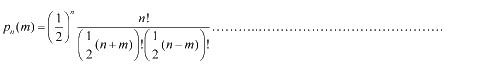 (1.1) (1.1)
To simplify equation (1.1), for m<<n, we obtain 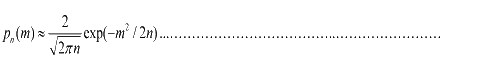 (1.2) (1.2)
Taking x to be a continuous variable, we can obtain 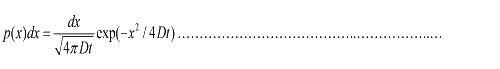 (1.3) (1.3)
where
v= l/τ was the average speed of the cell movement, and f=1/τ was the tumbling frequency of E.coli. In two dimensions, the square of the distance from the origin to the point (x, y) was r2=x2+y2; therefore For a macroscopic view, D was defined as the diffusion coefficient. For a simple diffusion process, it is easy to write an diffusion equation to describe the density ρ distribution. 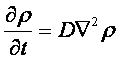 ...................................................................................................(1.4) ...................................................................................................(1.4)
Normally, as the swimming speed of E.coli is about 20um/s and the tumbling frequency is about 1 Hz, the diffusion coefficient is about 200um2/s [3].
Front propagation for cell growth
|
|
Density Dependent Motility
In experiments, we designed a circuit that the cell motility was repressed by cell density ρ. When the cell density ρ was high, the diffusion coefficient D became small. Therefore, the fisher’s equation as equation (2.1) was not valid in this case any more.
In order to be simple, we firstly considered the one dimension problem again. We assumed the cell density at point x was ρ(x) at time t. In a very short time τ, there would be two groups of cell at x moving into its nearby points x-δ, x+δ, due to the random walk. And the amount of cell in each group were proportional to the product of D(ρ(x)) and ρ(x). Therefore,
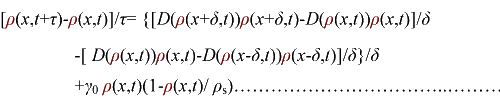 (3.1)
(3.1)
In the limit τ-->0 and δ-->0, we obtain
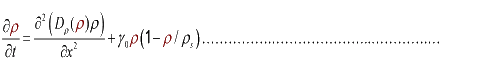 (3.2)
(3.2)
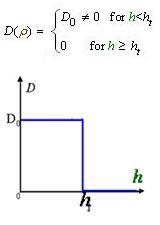
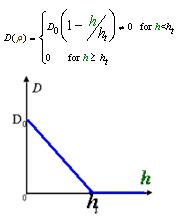
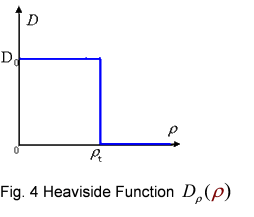
And the functionDρ(ρ) was a decrease function. For a simplest case, we considered a Heaviside Function(Fig.4). There was a threshold of cell density above which the cell can not swim forward but always tumble in the same place. Considering five points with the different cell denisty, among which there were group cell swimming to the nearby sites, we assumed that only the cell density in the middle of which was larger than the threshold. Then the cell in the middle would not go out of it. At the same time, the cell nearby would incessantly come into this point. As a result, the cell density here would increase, while the cell density nearby would continually decrease until zero.
 |
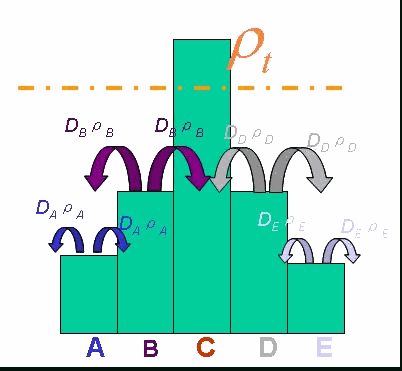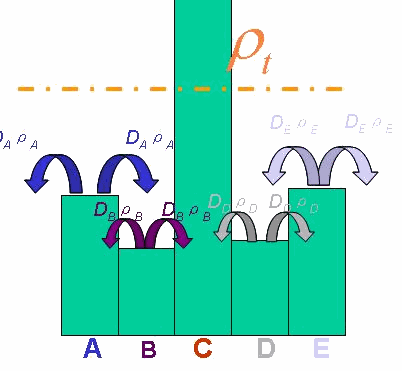 |
The numerical simulations gave us the results shown in Fig.5. The cell density showed a periodical-narrow-peak structure. These peaks were what we wanted, as they produced some regions of low cell density, though the whole pattern was not quite similar with that of experiments. And the exact pattern would come out when we took account of the other parts in the whole genetic circuit(See Full Model).
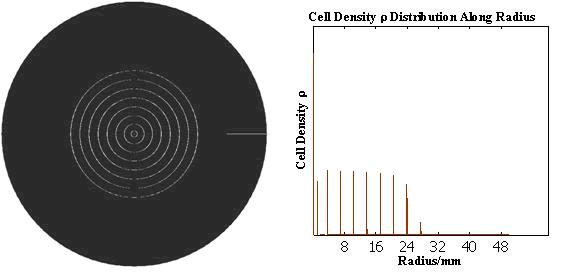
Full Model of Density Dependent Motility
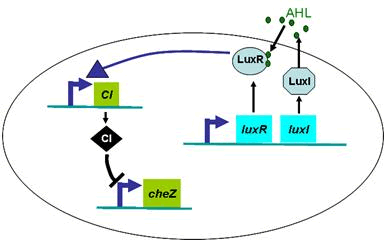
Actually, in our genetic circuit, we transformed a plasmid which can secrete AHL to environment (Fig.6). When the AHL density h of environment was high, the AHL came into the cell. Then AHL combining with LuxR repressed the expression level of cheZ which controled the motility of E.coli. So it was necessary to take account of the AHL effect.
First, the AHL was synthesized by the E.coli cell at the rate λ. And the degradation rate β of AHL whose half life is normally about 15 to 30 minutes. Considering the diffusion of AHL, we obtained
 (4.1)
(4.1)
where Dh is the diffusion coefficient of AHL, which is about 0.001mm2/min[6].
And the cell diffusion coefficient of E.coli is determined by the density of AHL. Therefore
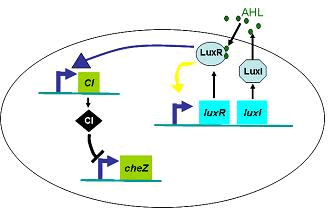
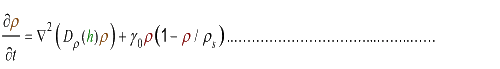 (4.2)
(4.2)
whereDρ(h) is a decreasing function of h.
Furthermore, the nutrient consumption influences the growth rate of E.coli. Therefore
 (4.3)
(4.3)
where n is the nutrient concentration.
For the nutrient, we made an assumption that the amount of nutrient consumed were proportional to the amount of cell increasing. Taking account of the nutrient diffusion, we had
 (4.4)
(4.4) We used several possible forms of functionDρ(h)(see Results Section2). The results showed that if the cell diffusion coefficient decreases fast near the AHL density threshold, the pattern came out as a multiple-ring one(Results Section2 (a),(e)). On the contrary, there was only one-ring pattern.
Therefore, in order to to make this curveDρ(h) decreasing sharply near the threshold, it followed a prediction that we can get a multiple-ring pattern by making an auto-activate genetic circuit which the combination of LuxR and AHL can activate the expression level of itself.
Furthermore, we did some two-spot patterns which initially have two points of E.coli cell, so as to compare with the experiments culture (Results Section3).
Modeling Results
In the simulation, we tried different values of undetermined parameters which were possible to change in experiments, to see how they influenced the pattern. Generally, we can vary the parameters of cell growth and cell motility which, in experiments, are easy to change. So we list the results of varying several parameters in the cell growth part and cell motility part.
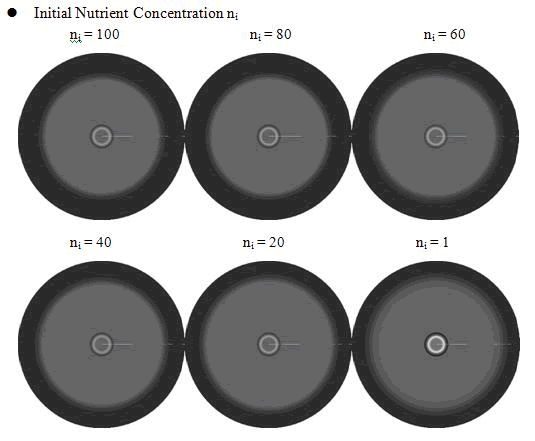
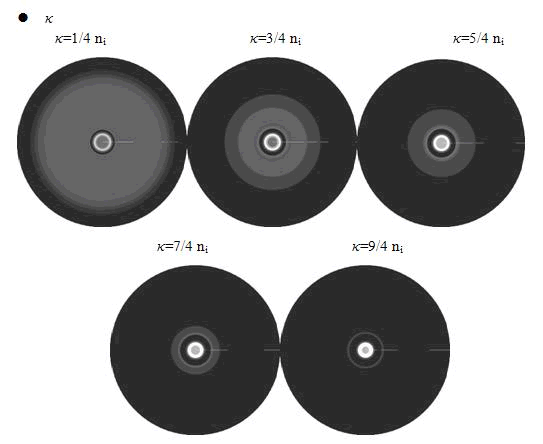
In the cell growth term, we considered the growth rate was related to nutrient concentration. When the nutrient was consumed by the cell, the grow rate of the cell would decrease (Fig. 7). There was a maximum growth rate γ0, when the nutrient was rich. The parameter κ described the sharp of this curve(Fig. 7). The larger κ gave us more smooth increasing curve. And we made an assumption that one unit of nutrient would change to cell number with a ratio k. Also in the initial condition, the nutrient concentration ni can influence the patterns. Therefore, the effects of all the four parameters were studied in our model.
Above reuslts indicated that, the faster cell growth (larger γ0 and smaller doubling time) formed a smaller and a little more unclear ring pattern. And the inner ring diameter would become a litter more large when the growth rate increased.
From above figures, it was found that the initial nutrient concentration ni had little influence to the pattern, especially when it was large. The only effect we observed was that smaller initial nutrient concentration ni made the ring slightly wider and more clear.
Here, the value of κ was related to the initial nutrient concentration ni . When initial nutrient concentration ni was fixed, a smaller κ parameter gave us the similar results with that of faster cell growth.
When we increased the value of k, the patterns did not change a lot, but only became a little more clearly.
In conclusion, the simulation results showed that the parameters of maximum growth rate γoand κ had a more important role on the ring-like pattern. And the other two parameters k and ni did not influence the pattern much.
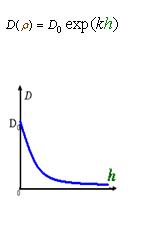
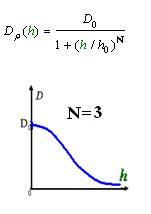
2. Cell Motility Dρ(h)
As Dρ(h) was a decreasing function of h, the possible formed of it can be
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The above movies showed that if the cell diffusion coefficient decreases fast near the AHL density threshold, the pattern came out as a multiple-ring one(Results Section2 (a),(e)). On the contrary, there was only one-ring pattern(Results Section2 (b),(c),(d)).
With the initial conditions of two or more spots, we obtained the below funny patterns which are amazing similar with that of experiments(results).

- [1] P.K.Pathria, Statistical Mechanics (Pergamon Press, Headington Hill Hall, Oxford; 1972)
- [2] Howard C.Berg, Random Walks in Biology (Princeton University Press, Princeton, Hew Jersey; 1993)
- [3] Nikhil Mittal, et al, Proc Natl Acad Sci 100, 13259 (2003)
- [4] R. A. Fisher, Ann. Eugenics 7, 353 (1937)
- [5] A.H.Bokhari, et al., Nonlinear Analysis (In Press)
- [6]Basu S, et al., Nature 434, 1130(2005)
- [7]J.W. Costerton, Naomi Balaban, Control of Biofilm Infections by Signal Manipulation (Springer,2008)
 "
"
 ,
,