Team:Imperial College/Motility Control
From 2008.igem.org
m |
m |
||
| (One intermediate revision not shown) | |||
| Line 11: | Line 11: | ||
{{Pipe}}} | {{Pipe}}} | ||
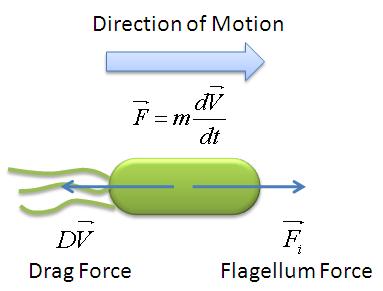
| - | We modelled the motility of motile ''B.subtilis'' using a mechanical model as shown above. Using experimental data from cell tracking, we were able to extract parameters which describe the model. The model and its parameters are defined [[Team:Imperial_College/Motility| '''here''']]. In summary, parameter ''A'' is the ratio of flagellum force to medium viscosity. It also represents the velocity of the cell after a sufficiently long time has elapsed, given that the flagellum force remains constant throughout its run. | + | We modelled the motility of motile ''B.subtilis'' using a mechanical model as shown above. Using experimental data from cell tracking, we were able to extract parameters which describe the model. The model and its parameters are defined [[Team:Imperial_College/Motility| '''here''']]. In summary, parameter ''A'' is the ratio of flagellum force to medium viscosity. It also represents the velocity of the cell after a sufficiently long time has elapsed, given that the flagellum force remains constant throughout its run. Parameter ''B'' is the initial velocity of the cell and ''alpha'' is the ratio of the vicosity of the medium to the cell's mass. |
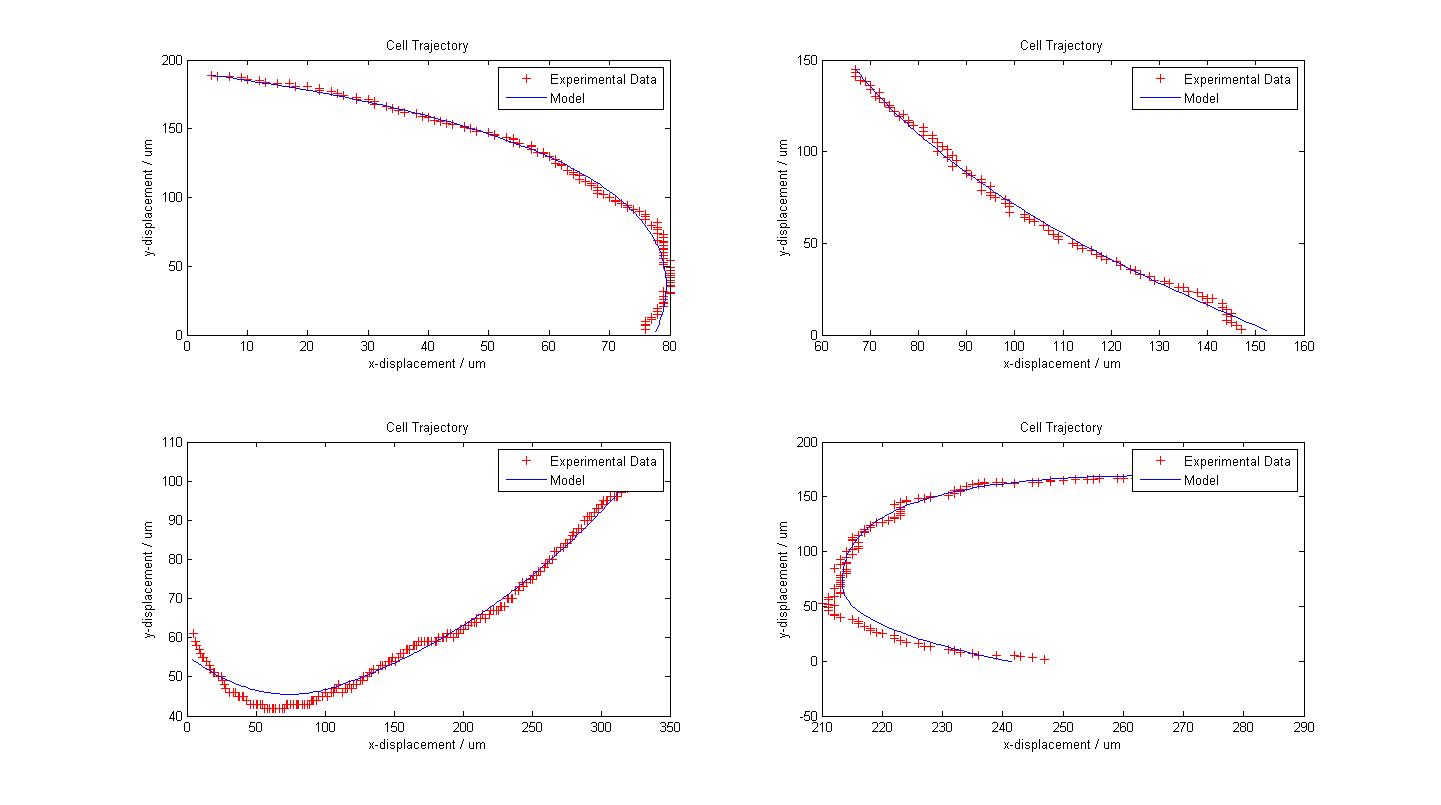
The following figure shows the results of our model fitting. We have introduced a change in flagellar force at certain points of the cell trajectory so as to achieve a better fit. A maximum of two runs were allowed for each cell trajectory. | The following figure shows the results of our model fitting. We have introduced a change in flagellar force at certain points of the cell trajectory so as to achieve a better fit. A maximum of two runs were allowed for each cell trajectory. | ||
| Line 23: | Line 23: | ||
{{Pipe}}} | {{Pipe}}} | ||
<br> | <br> | ||
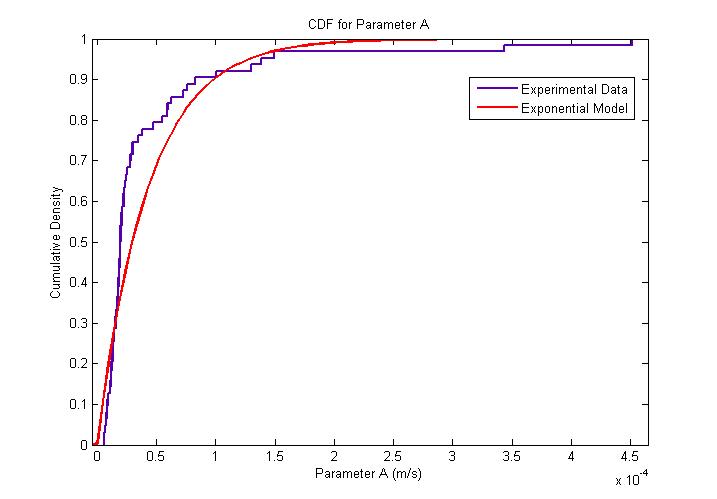
| - | The MATLAB Distribution Fitting Tool was used to model the distribution of parameter A, which is directly proportional to the | + | The MATLAB Distribution Fitting Tool was used to model the distribution of parameter A, which is directly proportional to the flagellar force, assuming that the medium is homogenous and its viscosity is constant throughout the medium. Parameter A was found to be exponentially distributed. The following figures describe the probability density function (PDF) and cumulative distribution function (CDF). |
{{{Pipe}} border{{Equals}}"0" cellpadding{{Equals}}"5" cellspacing{{Equals}}"0" align{{Equals}}"center" style{{Equals}}"background-color:transparent;color:#2B48B3;" | {{{Pipe}} border{{Equals}}"0" cellpadding{{Equals}}"5" cellspacing{{Equals}}"0" align{{Equals}}"center" style{{Equals}}"background-color:transparent;color:#2B48B3;" | ||
| Line 37: | Line 37: | ||
{{Imperial/Box2|Conclusion| | {{Imperial/Box2|Conclusion| | ||
| - | We fitted the data according to the simple mechanical model we have developed. From our model fitting process, we can see that | + | We fitted the data according to the simple mechanical model we have developed. From our model fitting process, we can see that flagellar force is exponentially distributed. Our mechanical model though simple, fits the cell trajectory data extremely well as shown in the figure above. Further work which can be done would be to utilise a movable stage to track the movement of ''B. subtilis'' over its entire run so as to obtain a distribution of other motility parameters associated running and tumbling events. |}} |
{{Imperial/EndPage|Major_Results|Major_Results}} | {{Imperial/EndPage|Major_Results|Major_Results}} | ||
Latest revision as of 01:58, 30 October 2008
Results of Motility Analysis
|
|||||||||||||||||||
 "
"