Team:Imperial College/Motility Control
From 2008.igem.org
m |
|||
| Line 23: | Line 23: | ||
{{Pipe}}} | {{Pipe}}} | ||
<br> | <br> | ||
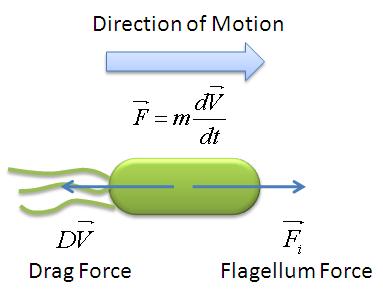
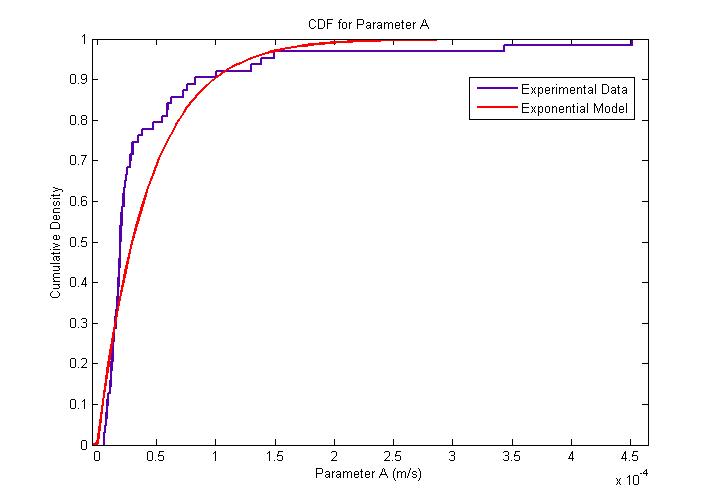
| - | The MATLAB Distribution Fitting Tool was used to model the distribution of parameter A, which is directly proportional to the flagellar force, assuming that the medium is homogenous and its viscosity is constant throughout the medium. Parameter A was | + | The MATLAB Distribution Fitting Tool was used to model the distribution of parameter A, which is directly proportional to the flagellar force, assuming that the medium is homogenous and its viscosity is constant throughout the medium. Parameter A was found to be exponentially distributed. The following figures describe the probability density function (PDF) and cumulative distribution function (CDF). |
{{{Pipe}} border{{Equals}}"0" cellpadding{{Equals}}"5" cellspacing{{Equals}}"0" align{{Equals}}"center" style{{Equals}}"background-color:transparent;color:#2B48B3;" | {{{Pipe}} border{{Equals}}"0" cellpadding{{Equals}}"5" cellspacing{{Equals}}"0" align{{Equals}}"center" style{{Equals}}"background-color:transparent;color:#2B48B3;" | ||
Latest revision as of 01:58, 30 October 2008
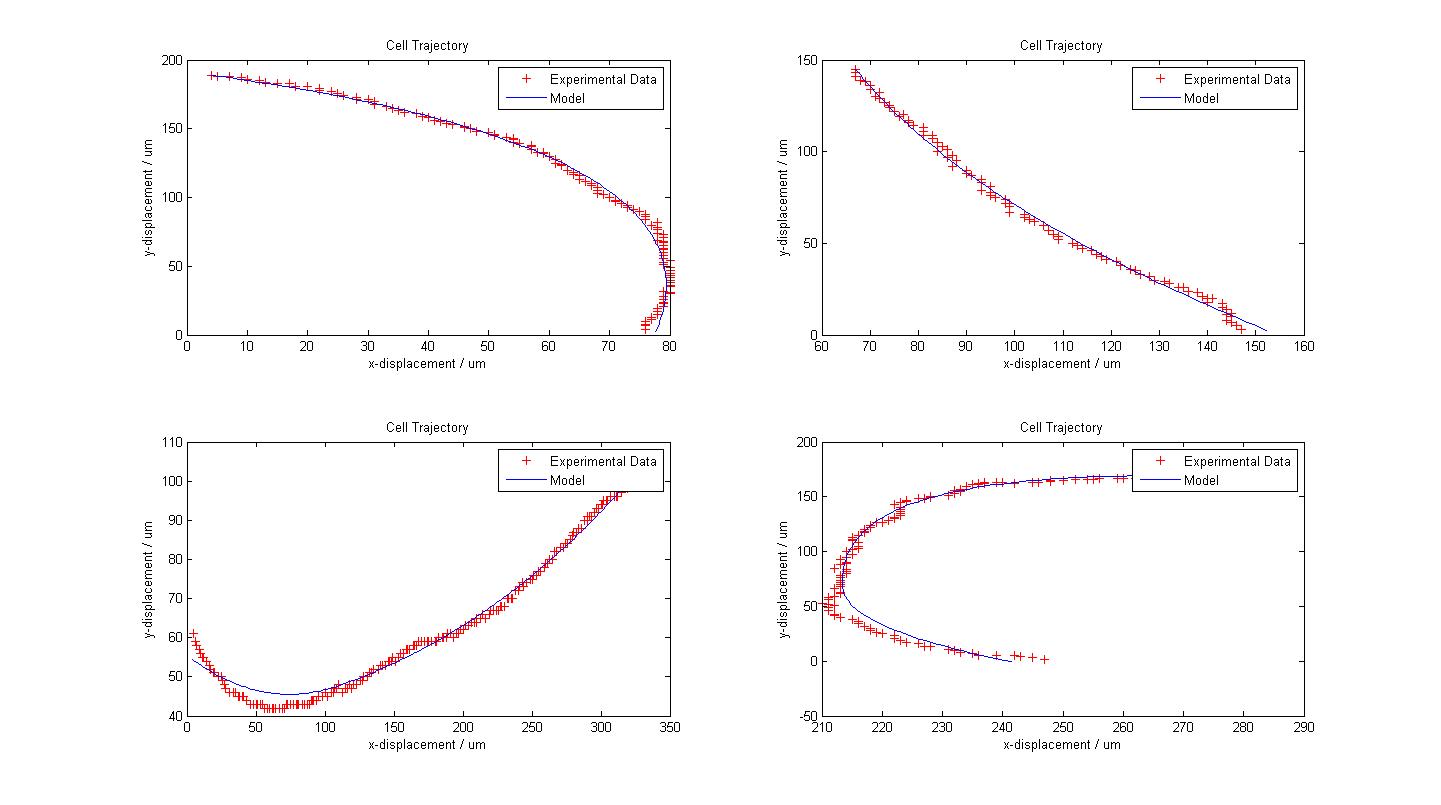
Results of Motility Analysis
|
|||||||||||||||||||
 "
"