Team:Imperial College/Genetic Circuit

From 2008.igem.org

(Difference between revisions)
m
m
Line 9: Line 9:
A simple [[Imperial_College/Courses/Spring2008/Synthetic_Biology/Computer_Modelling_Practicals/Practical_2 | synthesis-degradation model]] is assumed for the modelling of the expression of a protein under the control of a constitutive promoter, with the same model assumed for all four [[IGEM:IMPERIAL/2008/Prototype/Wetlab/test_constructs | promoter-RBS constructs]]. The synthesis-degradation model assumes a steady state level of mRNA.
A simple [[Imperial_College/Courses/Spring2008/Synthetic_Biology/Computer_Modelling_Practicals/Practical_2 | synthesis-degradation model]] is assumed for the modelling of the expression of a protein under the control of a constitutive promoter, with the same model assumed for all four [[IGEM:IMPERIAL/2008/Prototype/Wetlab/test_constructs | promoter-RBS constructs]]. The synthesis-degradation model assumes a steady state level of mRNA.
-
<math>\frac{d[protein]}{dt} = k_{1} - d_{1}[protein]</math>
+
<math>\frac{d[protein]}{dt} {{Equals}} k_{1} - d_{1}[protein]</math>
In this case, <math>[protein]</math> represents the concentration of GFP, <math>k_{1}</math> represents the rate of sythesis and <math>d_{1}</math> represents the degradation rate.
In this case, <math>[protein]</math> represents the concentration of GFP, <math>k_{1}</math> represents the rate of sythesis and <math>d_{1}</math> represents the degradation rate.
Line 19: Line 19:
We can also solve this ODE analytically. Consider the steady-state behaviour of <math>[protein]</math>.
We can also solve this ODE analytically. Consider the steady-state behaviour of <math>[protein]</math>.
-
<math>\frac{d[protein]}{dt}=0 \Rightarrow [protein]_{steady-state}=\frac{k_1}{d_1}</math>  
+
<math>\frac{d[protein]}{dt}{{Equals}}0 \Rightarrow [protein]_{steady-state}{{Equals}}\frac{k_1}{d_1}</math>  
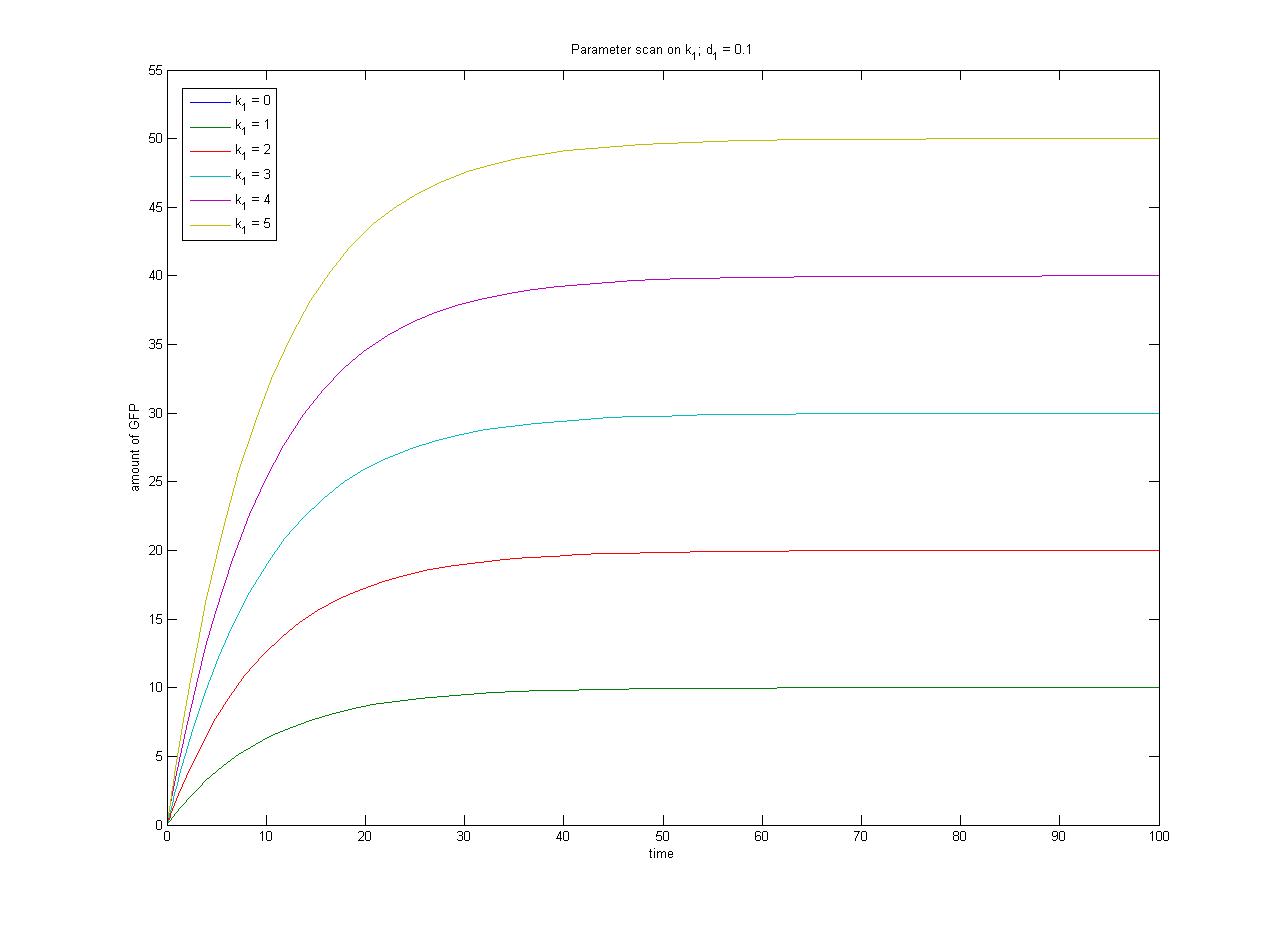
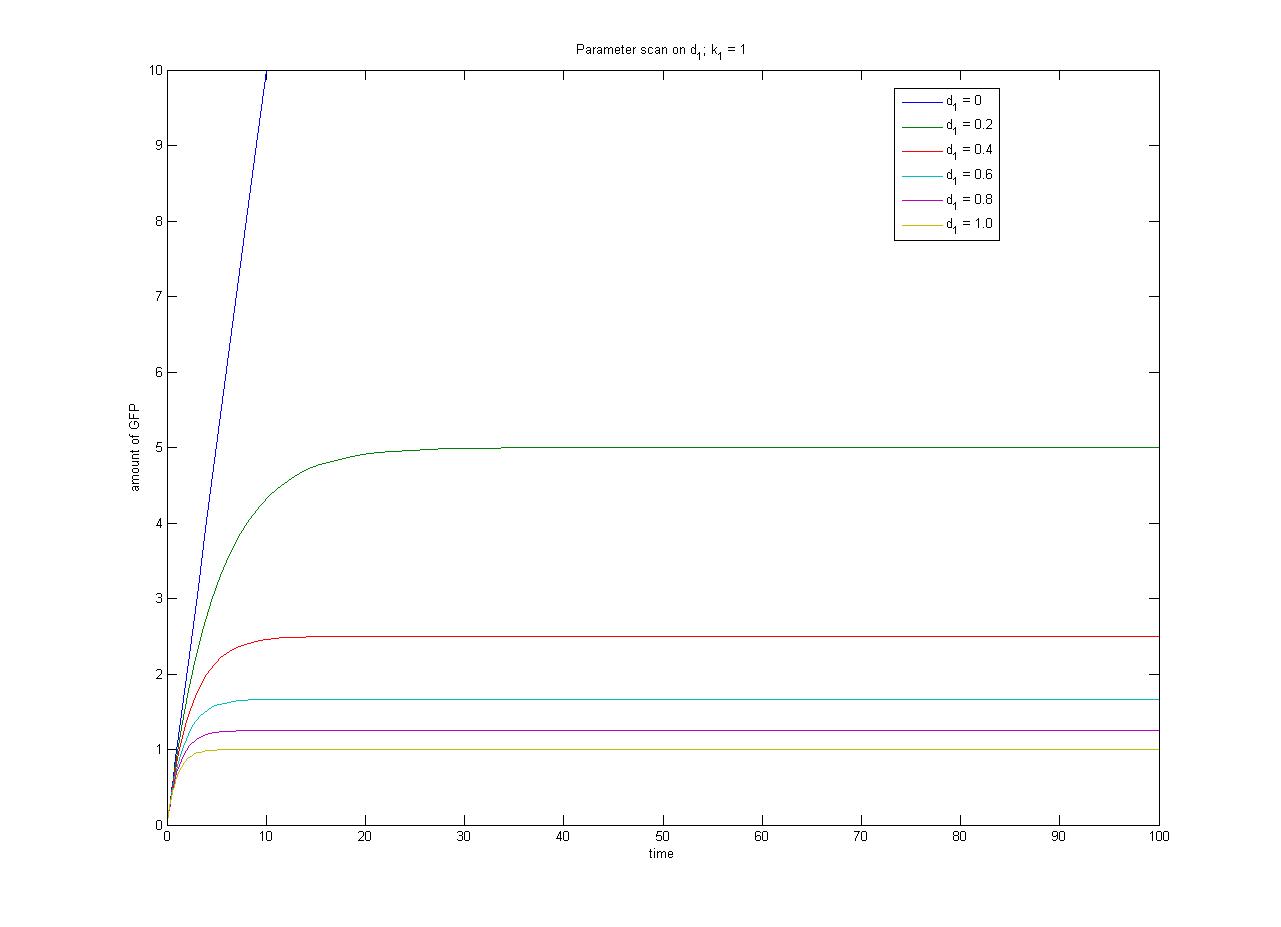
This relationship can be seen in the parameter scan graphs on the right.
This relationship can be seen in the parameter scan graphs on the right.
Line 26: Line 26:
<br>
<br>
Note from the parameter scan graphs:<br>
Note from the parameter scan graphs:<br>
-
*In the case where <math>k_1 = 0</math>, no GFP is sythesised.
+
*In the case where <math>k_1 {{Equals}} 0</math>, no GFP is sythesised.
-
*In the case where <math>d_1 = 0</math>, the concentration of protein does not reach a steady state.
+
*In the case where <math>d_1 {{Equals}} 0</math>, the concentration of protein does not reach a steady state.
|[[Image:Phase 1.PNG|thumb|300px|Constitutive expression of antibiotic resistance (AB) and GFP. GFP brick is part E0040, GFPmut3b. Terminator is part B0015, the double-stop.]]
|[[Image:Phase 1.PNG|thumb|300px|Constitutive expression of antibiotic resistance (AB) and GFP. GFP brick is part E0040, GFPmut3b. Terminator is part B0015, the double-stop.]]
-
<gallery caption="Parameter Scan" align="right">
+
<gallery caption{{Equals}}"Parameter Scan" align{{Equals}}"right">
Image:ParamterScanGFPk1.jpg|Parameter scan on <math>k_1</math>
Image:ParamterScanGFPk1.jpg|Parameter scan on <math>k_1</math>
-
Image:ParamterScanGFPd1.jpg|Parameter scan on <math>d_1</math>
+
Image:ParamterScanGFPd1.jpg|Parameter scan on <math>d_1</math></gallery>
-
</gallery>}}
+
}}
-
{{Imperial/Box1|Modelling Inducible Gene Expression|
+
{{Imperial/Box1|Modelling Inducible Gene Expression
-
[[Image:Phase 2-linduced.PNG|thumb|300px]]
+
|[[Image:Phase 2-linduced.PNG|thumb|300px]]
The repressor is constitutively expressed. Hence we can assume the constitutive expression model from the previous characterisation step.
The repressor is constitutively expressed. Hence we can assume the constitutive expression model from the previous characterisation step.
-
<math>\frac{d[R]}{dt} = k_{1} - d_{1}[R]</math>
+
<math>\frac{d[R]}{dt} {{Equals}} k_{1} - d_{1}[R]</math>
When the inducer is added it binds reversibly to the repressor.
When the inducer is added it binds reversibly to the repressor.
Line 48: Line 48:
Repressor only binds to the promoter when it is in its unbound form, hence transcription will be a function of free repressor concentration.
Repressor only binds to the promoter when it is in its unbound form, hence transcription will be a function of free repressor concentration.
-
<math> Transcription = \frac{\beta.{[R]}^n}{{K_m}^n+[R]^n}</math><br>
+
<math> Transcription {{Equals}} \frac{\beta.{[R]}^n}{{K_m}^n+[R]^n}</math><br>
And overall protein expression can be described as
And overall protein expression can be described as
-
<math>\frac{d[protein]}{dt} = Transcription - d_2[protein]</math>
+
<math>\frac{d[protein]}{dt} {{Equals}} Transcription - d_2[protein]</math>
The [[media:ConcentrationsODE.m|ODEs]] and [[media:SimulationconcentrationsODE.m|simulation]] may be found in the Appendices section of the Dry Lab hub.
The [[media:ConcentrationsODE.m|ODEs]] and [[media:SimulationconcentrationsODE.m|simulation]] may be found in the Appendices section of the Dry Lab hub.
<biblio>
<biblio>
-
#1 pmid=18612302
+
#1 pmid{{Equals}}18612302
</biblio>
</biblio>
}}
}}
{{Imperial/EndPage|Project|Motility}}
{{Imperial/EndPage|Project|Motility}}

Revision as of 00:39, 10 October 2008


The Genetic Circuit


An accurate mathematical description of the genetic circuit is essential for projects involving synthetic biology. Such descriptions are an integral component of part submission to the Registry, as exemplified by the canonical characterisation of part F2620 #1. The ability to capture part behaviour as a mathematical relationship between input and output is useful for future re-use of the part and modification of integration into novel genetic circuits.


Modelling Constitutive Gene Expression

A simple synthesis-degradation model is assumed for the modelling of the expression of a protein under the control of a constitutive promoter, with the same model assumed for all four promoter-RBS constructs. The synthesis-degradation model assumes a steady state level of mRNA.

<math>\frac{d[protein]}{dt} = k_{1} - d_{1}[protein]</math>

In this case, <math>[protein]</math> represents the concentration of GFP, <math>k_{1}</math> represents the rate of sythesis and <math>d_{1}</math> represents the degradation rate. We can easily simulate this synthesis-degradation model using matlab:
ODE
Simulation File

We can also solve this ODE analytically. Consider the steady-state behaviour of <math>[protein]</math>.

<math>\frac{d[protein]}{dt}=0 \Rightarrow [protein]_{steady-state}=\frac{k_1}{d_1}</math>

This relationship can be seen in the parameter scan graphs on the right.

From the wetlab experiments it is likely that we will obtain steady-state data for each of the four promoter-RBS constructs. If we assume the same rate of degradation of GFP in each case, we can have some measure of the relative rate of transcription through each promoter which will help us with the selection of the most appropriate promoter to use for Phase 2. In order to obtain an absolute measure of transcription (as opposed to a relative measure of transcriptional strength) we require constitutive expression in terms of molecules per cell (as opposed to fluorescene in arbitrary units).
Note from the parameter scan graphs:

  • In the case where <math>k_1 = 0</math>, no GFP is sythesised.
  • In the case where <math>d_1 = 0</math>, the concentration of protein does not reach a steady state.
Constitutive expression of antibiotic resistance (AB) and GFP. GFP brick is part E0040, GFPmut3b. Terminator is part B0015, the double-stop.

Parameter scan on <math>k_1</math>

Parameter scan on <math>d_1</math>


{{Imperial/Box1|Modelling Inducible Gene Expression

|
Phase 2-linduced.PNG

The repressor is constitutively expressed. Hence we can assume the constitutive expression model from the previous characterisation step.

<math>\frac{d[R]}{dt} = k_{1} - d_{1}[R]</math>

When the inducer is added it binds reversibly to the repressor.

<math> R + I \Leftrightarrow RI </math>

Repressor only binds to the promoter when it is in its unbound form, hence transcription will be a function of free repressor concentration.

<math> Transcription = \frac{\beta.{[R]}^n}{{K_m}^n+[R]^n}</math>

And overall protein expression can be described as

<math>\frac{d[protein]}{dt} = Transcription - d_2[protein]</math>

The ODEs and simulation may be found in the Appendices section of the Dry Lab hub.

<biblio>

  1. 1 pmid=18612302

</biblio> }}


Retrieved from "http://2008.igem.org/Team:Imperial_College/Genetic_Circuit"