Team:Imperial College/Genetic Circuit
From 2008.igem.org
m |
m |
||
| Line 54: | Line 54: | ||
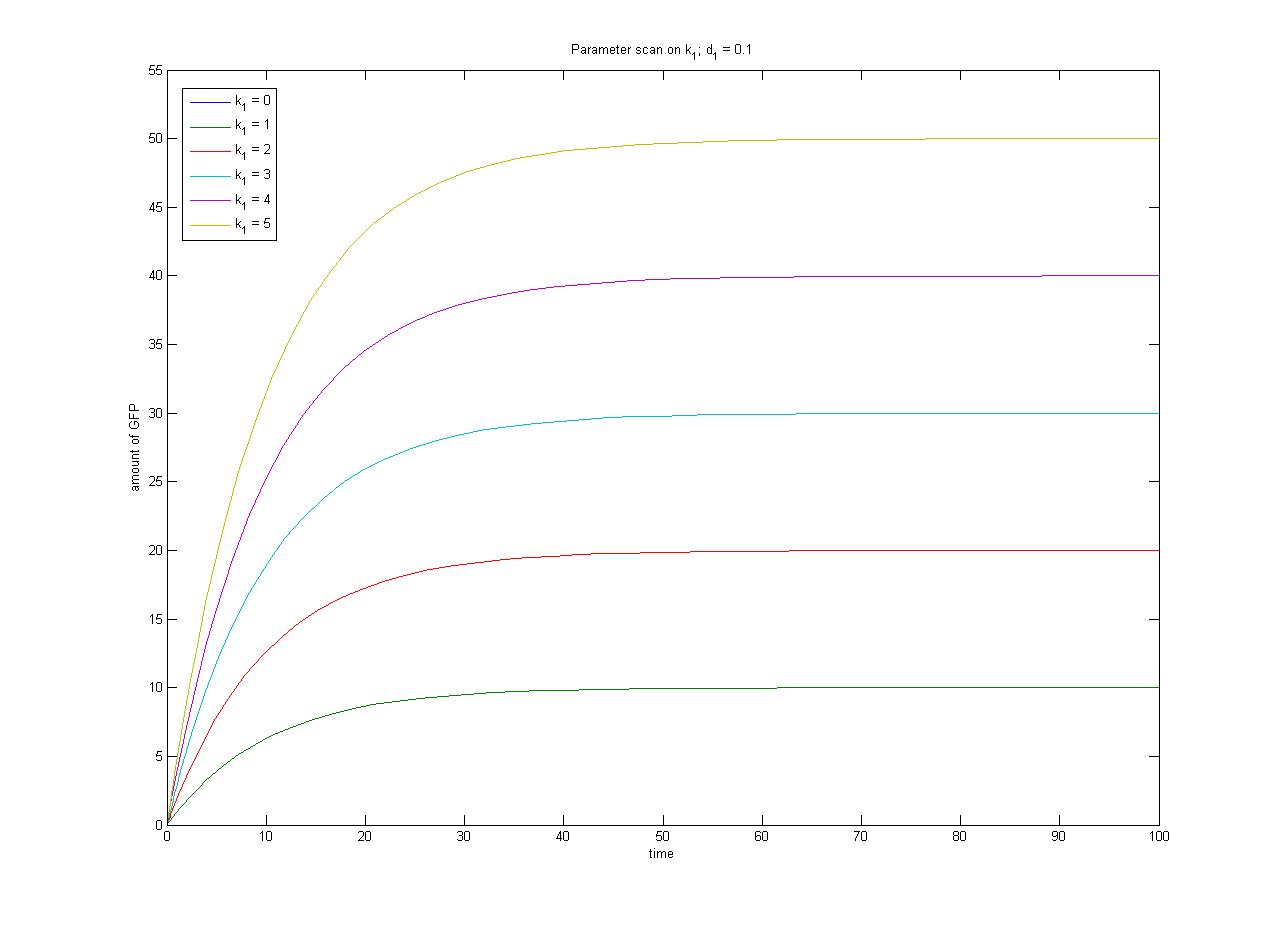
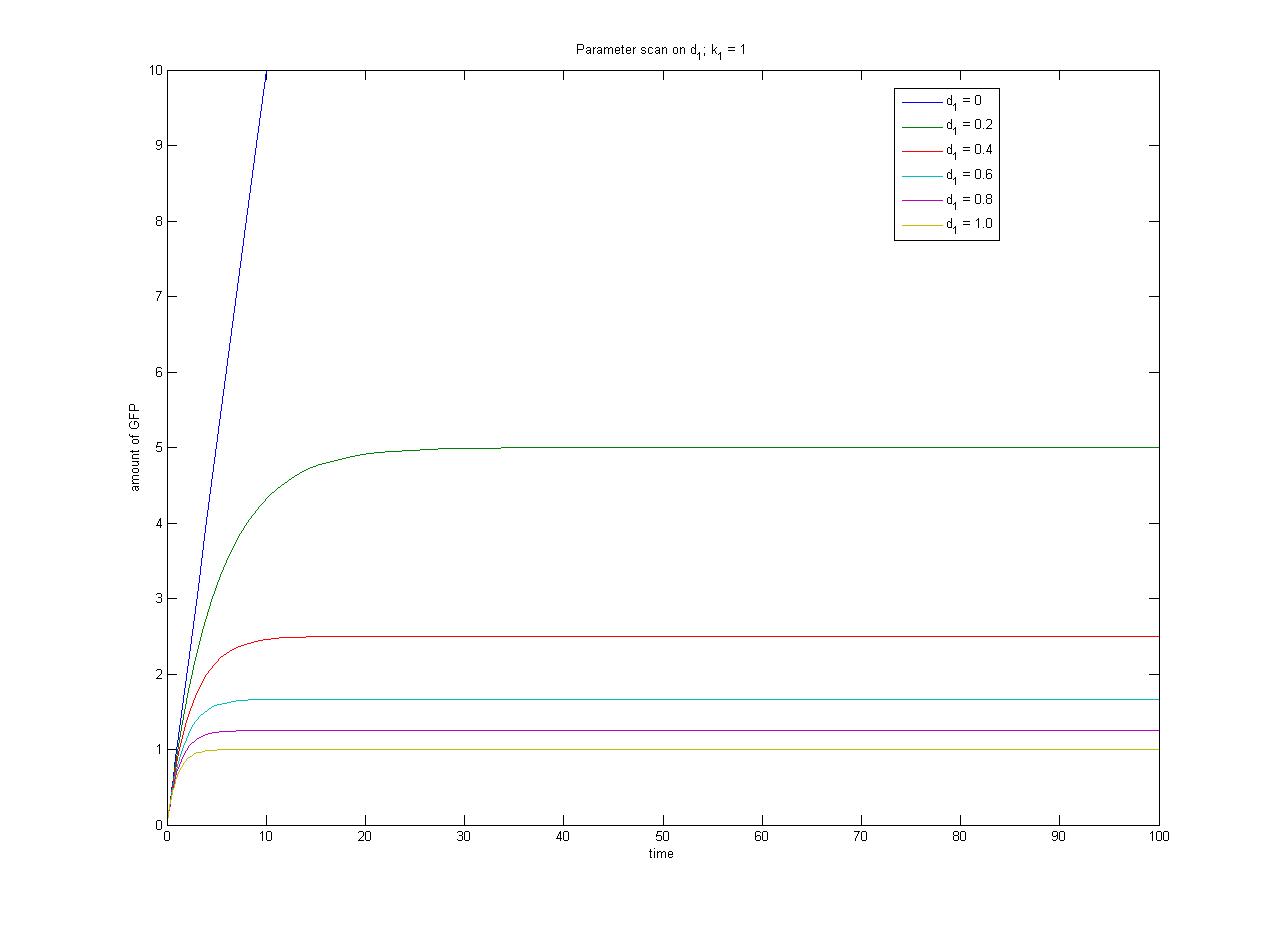
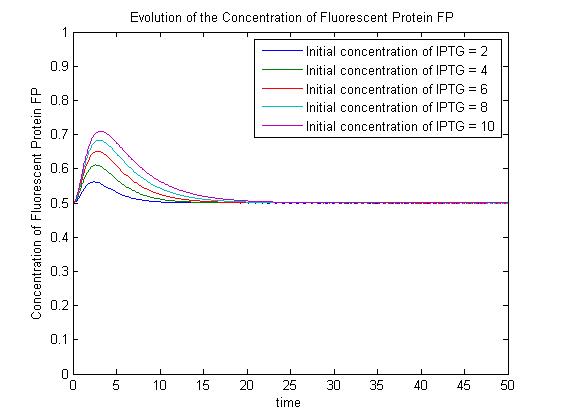
The [[media:ConcentrationsODE.m|ODEs]] and [[media:SimulationconcentrationsODE.m|simulation]] may be found in the Appendices section of the Dry Lab hub. | The [[media:ConcentrationsODE.m|ODEs]] and [[media:SimulationconcentrationsODE.m|simulation]] may be found in the Appendices section of the Dry Lab hub. | ||
| - | |||
| - | |||
}} | }} | ||
Revision as of 16:06, 21 October 2008
Modelling the Genetic Circuit
|
|||||||||||||||||||||||||
 "
"