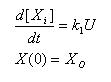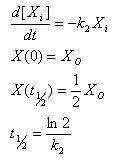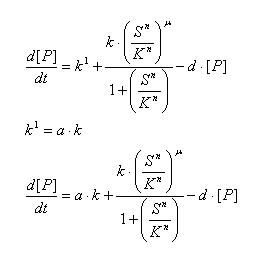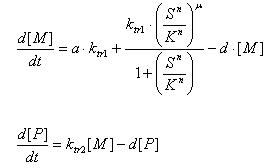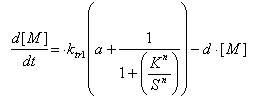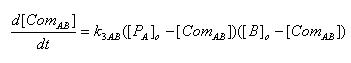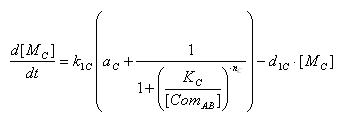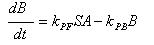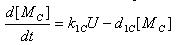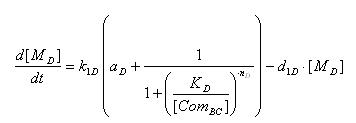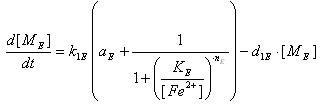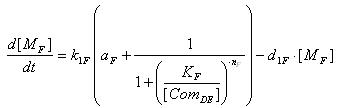Team:NTU-Singapore/Modelling/ODE
From 2008.igem.org
(→ODEs used in modeling) |
Lalala8585 (Talk | contribs) (→Phosphorylation and Dephosphorylation) |
||
| Line 46: | Line 46: | ||
==Phosphorylation and Dephosphorylation== | ==Phosphorylation and Dephosphorylation== | ||
Assumptions: | Assumptions: | ||
| - | *Linear | + | *Linear kinetic rate laws apply only if XT is much less than the Michaelis constants of both kinase and phosphotase |
| - | [[Image:Phosphorylation.JPG|200px|Phosphorylation and Dephosphorylation]]<br> | + | [[Image:Phosphorylation.JPG|200px||thumb|center|Phosphorylation and Dephosphorylation]]<br> |
| - | + | <center> | |
| - | XT : total cost of X protein in phosphorylated and unphosphorylated form | + | {|border="0"| |
| - | S : | + | |XT : |
| - | k2 : | + | |total cost of X protein in phosphorylated and unphosphorylated form |
| - | + | |- | |
| + | |S : | ||
| + | |protein kinase concentration | ||
| + | |- | ||
| + | |k2 : | ||
| + | |accounts for protein phosphotase | ||
| + | |} | ||
| + | </center> | ||
*Modeled after simple linear kinetics | *Modeled after simple linear kinetics | ||
*Gives a hyperbolic signal response curve when X plotted vs S | *Gives a hyperbolic signal response curve when X plotted vs S | ||
Revision as of 02:13, 25 October 2008
|
Contents |
ODEs used in modeling
In this section, we will have a short discussion on the ODEs used for Deterministic Modeling in our iGem project.
For the modeling exercise, we use mainly simple linear ODEs to describe the system we have at hand. These ODEs are used to describe processes such as constitutive transcription/ translation etc. Nonlinear equations are used for more complex processes such as regulated transcription. The choice of these equations are in hope that they can describe the system to a relative degree of accuracy and yet be simple enough to be solved. This is very much an engineering compromise between a rigorous description and getting an answer that is good enough which is required.
Our systems are based on the assumptions that Lumped parameter models are sufficient to describe them.
Lumped parameter models are those in which spatial variations are ignored and the dependent variables are uniform throughout the whole system. The only variations are those with respect to time leading to mathematical description in terms of the ODEs used.
The following equations shows the break down of the different equations that will be used in this modeling exercise. By understanding this section, it would make the understanding of the system of ODEs used in our iGEm modeling exercise.
Constant synthesis & Linear Synthesis
- Simple ode to describe constant synthesis
- Gives an explicit analytical solution
- Unique solution once a IC is posed
Linear Degradation
- Rate of degradation is proportional to how much of the molecule is present
- Gives an explicit analytical solution
- Constant half life
Simple Forward Reaction
[C] : Complex
kc : Rate constant of complex formation
This equation ignores the fact that dissociation of the complex occurs. We can do so if the dissociation is much slower than the formation.
- Single solvable equation for the unknown C
- Simple, unique solution available with I.C
Phosphorylation and Dephosphorylation
Assumptions:
- Linear kinetic rate laws apply only if XT is much less than the Michaelis constants of both kinase and phosphotase
| XT : | total cost of X protein in phosphorylated and unphosphorylated form |
| S : | protein kinase concentration |
| k2 : | accounts for protein phosphotase |
- Modeled after simple linear kinetics
- Gives a hyperbolic signal response curve when X plotted vs S
Regulated Transcription
[P]: Protein Formed
µ: Repression, µ=0;
Activation, µ=1
K: Hill Constant Value of input that gives 50% response
n: Hill coefficient Slope of signal-response curve at this input signal
d: degradation of protein
k1: basal gene expression
k: signal-dependent gene expression
a: correlation between k1 and k, 0<a<1
This ODE attempts to capture characteristics of the mRNA dynamics
For our modeling, all our detection systems activates some form of transcription. Therefore µ=1 in all cases for our modeling exercise.
ODE system used in model
The system can be viewed as two parts. The first part comprises of lactose induced production of colicin E7 and the immunity protein. The second part comprises of a detection mechanism that produces the lysis protein upon the detection of both Iron ions and Ai-2 ( Autoinducer 2).
Lactose controlled production of E7 + Imm
Variables
- LacI = A
- Lactose =B
- E7 = C
- LacI production
- Transcription of LacI gene mRNA
[MA] : LacI mRNA concentration
k1A : kinetic constant of transcription
U : system input
d1A : degradation constant for mRNA
- Translation of LacI Protein
[PA] : Protein concentration
k2A : kinetic constant of translation
d2A : degradation constant for Protein
- Complex formation between LacI and Lactose
[ComAB] : Complex of LacI and Lactose
K3AB : Rate constant of complex formation
[PA]o : Protein concentration of LacI at the time of Lactose addition
[B]o : Initial concentration of Lactose
- E7 production
- Transcription of E7 gene mRNA
[MC]: E7 mRNA Concentration
k1C: kinetic constant of transcription
a : constitutive portion , 0<a<1
KC: Hill constant
nC: Hill coefficient
d1C: degradation constant for mRNA
- Translation of E7 Protein
[PC] : Protein concentration
k2C : kinetic constant of translation
d2C : degradation constant for Protein
Iron and Ai2 controlled production of Lysis
Variables
Variables
- Ai-2 : A
- ai-2-phos : B
- LsrR : C
- SupD derivatives : D
- T7ptag : E
- Lysis : F
- Phosphorylation of ai-2
A: Ai-2
B: Ai-2-phos
kPF: Forward Phosphorylation
S: Concentration of Protein Kinase
kPB: Backward dephosphorylation
- LsrR production
- Transcription of LsrR gene mRNA
[MC]: LacI mRNA concentration
k1C : kinetic constant of transcription
U : system input
d1C: degradation constant for mRNA,br>
- Translation of LsrR protein
[PC] : Protein concentration
k2C : kinetic constant of translation
d2C : degradation constant for Protein
- Complex formation between Ai-2-phos and LsrR
[ComAB] : Complex of LsrR and Ai-2-phos
k3BC : Rate constant of complex formation
[PC]o: Protein concentration of LsrR at the time of start of complex formation
[B]o: Initial concentration of Ai-2-phos
The hard part here is to determine what is the initial concentration of the protein LsrR and Ai-2-phos. A way out of this mess is to simplify the equation even more.
- AND GATE odes
- Transcription of SupD gene mRNA
[MD]: t7 mRNA Concentration
k1D: kinetic constant of transcription
a : constitutive portion , 0<a<1
KD: Hill constant
nD: Hill coefficient
d1D: degradation constant for mRNA
- Transcription of T7ptag gene mRNA
[ME]: supD mRNA Concentration
k1E: kinetic constant of transcription
a : constitutive portion , 0<a<1
KE: Hill constant
nE: Hill coefficient
d1E: degradation constant for mRNA
- Complex formation between tRNA and mRNA
[ComDE] : Complex of tRNA and mRNA t7
k3DE : Rate constant of complex formation
[MD]o : concentration of tRNA at the time of start of complex formation
[ME]o : Initial concentration of mRNA t7
- Translation of t7 protein
[PF] : Protein concentration
k2F : kinetic constant of translation
d2F : degradation constant for Protein
- Lysis
- Transcription of Lysis gene mRNA
[MF]: Lysis mRNA Concentration
k1F: kinetic constant of transcription
a : constitutive portion , 0<a<1
KF: Hill constant
nF: Hill coefficient
d1F: degradation constant for mRNA
- Translation of Lysis protein
[PF] : Protein concentration
k2F : kinetic constant of translation
d2F : degradation constant for Protein
 "
"