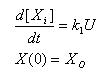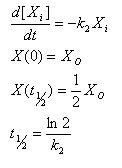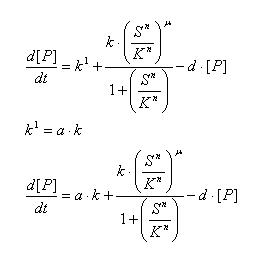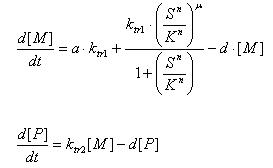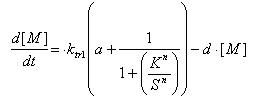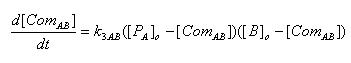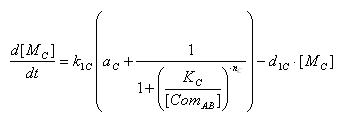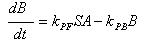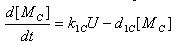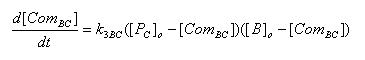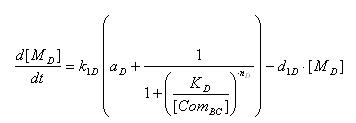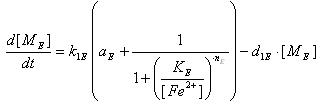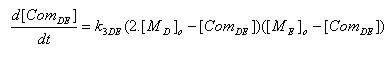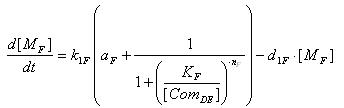Team:NTU-Singapore/Modelling/ODE
From 2008.igem.org
Lalala8585 (Talk | contribs) (→Iron and Ai2 controlled production of Lysis) |
Lalala8585 (Talk | contribs) (→Complex formation between Ai-2-phos and LsrR) |
||
| Line 270: | Line 270: | ||
===Complex formation between Ai-2-phos and LsrR=== | ===Complex formation between Ai-2-phos and LsrR=== | ||
| - | [[Image:Complex2.JPG | | + | [[Image:Complex2.JPG |350px|Complex2]]<br> |
{|border="0"| | {|border="0"| | ||
|[ComAB] : | |[ComAB] : | ||
| Line 285: | Line 285: | ||
|} | |} | ||
| - | The hard part here is to determine what is the initial concentration of the protein LsrR and Ai-2-phos. A way out of this mess is to simplify the equation even more. | + | The hard part here is to determine what is the initial concentration of the protein LsrR and Ai-2-phos. A way out of this mess is to simplify the equation even more. |
===AND GATE odes=== | ===AND GATE odes=== | ||
Revision as of 02:57, 25 October 2008
|
Contents |
ODEs used in modeling
In this section, we will have a short discussion on the ODEs used for Deterministic Modeling in our iGem project.
For the modeling exercise, we use mainly simple linear ODEs to describe the system we have at hand. These ODEs are used to describe processes such as constitutive transcription/ translation etc. Nonlinear equations are used for more complex processes such as regulated transcription. The choice of these equations are in hope that they can describe the system to a relative degree of accuracy and yet be simple enough to be solved. This is very much an engineering compromise between a rigorous description and getting an answer that is good enough which is required.
Our systems are based on the assumptions that Lumped parameter models are sufficient to describe them.
Lumped parameter models are those in which spatial variations are ignored and the dependent variables are uniform throughout the whole system. The only variations are those with respect to time leading to mathematical description in terms of the ODEs used.
The following equations shows the break down of the different equations that will be used in this modeling exercise. By understanding this section, it would make the understanding of the system of ODEs used in our iGEm modeling exercise.
Constant synthesis & Linear Synthesis
- Simple ode to describe constant synthesis
- Gives an explicit analytical solution
- Unique solution once a IC is posed
Linear Degradation
- Rate of degradation is proportional to how much of the molecule is present
- Gives an explicit analytical solution
- Constant half life
Simple Forward Reaction
[C] : Complex
kc : Rate constant of complex formation
This equation ignores the fact that dissociation of the complex occurs. We can do so if the dissociation is much slower than the formation.
- Single solvable equation for the unknown C
- Simple, unique solution available with I.C
Phosphorylation and Dephosphorylation
Assumptions:
- Linear kinetic rate laws apply only if XT is much less than the Michaelis constants of both kinase and phosphotase
| XT : | total cost of X protein in phosphorylated and unphosphorylated form |
| S : | protein kinase concentration |
| k2 : | accounts for protein phosphotase |
- Modeled after simple linear kinetics
- Gives a hyperbolic signal response curve when X plotted vs S
Regulated Transcription
| [P]: | Protein Formed |
| µ: | Repression, µ=0; Activation, µ=1 |
| K: | Hill Constant Value of input that gives 50% response |
| n: | Hill coefficient Slope of signal-response curve at this input signal |
| d: | degradation of protein |
| k1: | basal gene expression |
| k: | signal-dependent gene expression |
| a: | correlation between k1 and k, 0<a<1 |
This ODE attempts to capture characteristics of the mRNA dynamics
For our modeling, all our detection systems activates some form of transcription. Therefore µ=1 in all cases for our modeling exercise.
ODE system used in model
The system can be viewed as two parts. The first part comprises of lactose induced production of colicin E7 and the immunity protein. The second part comprises of a detection mechanism that produces the lysis protein upon the detection of both Iron ions and Ai-2 ( Autoinducer 2).
Lactose controlled production of E7 + Imm
Variables
| LacI = | A |
| Lactose = | B |
| E7 = | C |
LacI production
- Transcription of LacI gene mRNA
| [MA]: | LacI mRNA concentration |
| k1A: | kinetic constant of transcription |
| U: | system input |
| d1A: | degradation constant for mRNA |
- Translation of LacI Protein
| [PA]: | Protein concentration |
| k2A: | kinetic constant of translation |
| d2A: | degradation constant for Protein |
Complex formation between LacI and Lactose
| [ComAB] : | Complex of LacI and Lactose |
| K3AB : | Rate constant of complex formation |
| [PA]o : | Protein concentration of LacI at the time of Lactose addition |
| [B]o : | Initial concentration of Lactose |
E7 production
- Transcription of E7 gene mRNA
| [MC]: | E7 mRNA Concentration |
| k1C: | kinetic constant of transcription |
| a : | constitutive portion , 0<a<1 |
| KC: | Hill constant |
| nC: | Hill coefficient |
| d1C: | degradation constant for mRNA |
- Translation of E7 Protein
| [PC] : | Protein concentration |
| k2C : | kinetic constant of translation |
| d2C : | degradation constant for Protein |
Variables of Iron and Ai2 controlled production of Lysis
Variables
| #Ai-2: | A |
| #ai-2-phos: | B |
| #LsrR: | C |
| #SupD derivatives: | D |
| #T7ptag: | E |
| #Lysis: | F |
Phosphorylation of Ai-2
| A: | Ai-2 |
| B: | Ai-2-phos |
| kPF: | Forward Phosphorylation |
| S: | Concentration of Protein Kinase |
| kPB: | Backward dephosphorylation |
LsrR production
- Transcription of LsrR gene mRNA
| [MC]: | LacI mRNA concentration |
| k1C: | kinetic constant of transcription |
| U: | system input |
| d1C: | degradation constant for mRNA |
- Translation of LsrR protein
| [PC] : | Protein concentration |
| k2C: | kinetic constant of translation |
| d2C: | degradation constant for Protein |
Complex formation between Ai-2-phos and LsrR
| [ComAB] : | Complex of LsrR and Ai-2-phos |
| k3BC : | Rate constant of complex formation |
| [PC]o: | Protein concentration of LsrR at the time of start of complex formation |
| [B]o: | Initial concentration of Ai-2-phos |
The hard part here is to determine what is the initial concentration of the protein LsrR and Ai-2-phos. A way out of this mess is to simplify the equation even more.
AND GATE odes
- Transcription of SupD gene mRNA
| [MD]: | t7 mRNA Concentration | ||
| k1D: | kinetic constant of transcription | a : | constitutive portion , 0<a<1 |
| KD: | Hill constant | ||
| nD: | Hill coefficient | ||
| d1D: | degradation constant for mRNA |
- Transcription of T7ptag gene mRNA
| [ME]: | supD mRNA Concentration |
| k1E: | kinetic constant of transcription |
| a : | constitutive portion , 0<a<1 |
| KE: | Hill constant |
| nE: | Hill coefficient |
| d1E: | degradation constant for mRNA |
- Complex formation between tRNA and mRNA
| [ComDE] : | Complex of tRNA and mRNA t7 |
| k3DE : | Rate constant of complex formation |
| [MD]o : | concentration of tRNA at the time of start of complex formation |
| [ME]o : | Initial concentration of mRNA t7 |
- Translation of t7 protein
| [PF] : | Protein concentration |
| k2F : | kinetic constant of translation |
| d2F : | degradation constant for Protein |
Lysis production
- Transcription of Lysis gene mRNA
| [MF]: | Lysis mRNA Concentration | ||
| k1F: | kinetic constant of transcription | a : | constitutive portion , 0<a<1 |
| KF: | Hill constant | ||
| nF: | Hill coefficient | ||
| d1F: | degradation constant for mRNA |
- Translation of Lysis protein
| [PF] : | Protein concentration |
| k2F : | kinetic constant of translation |
| d2F : | degradation constant for Protein |
 "
"