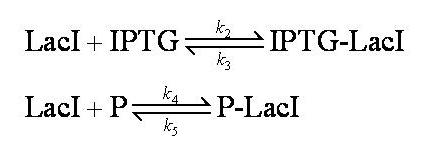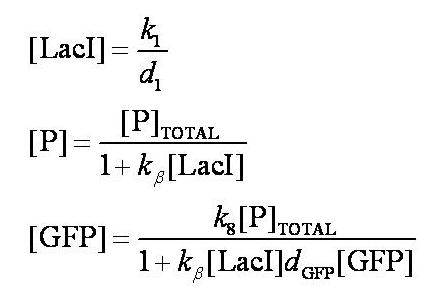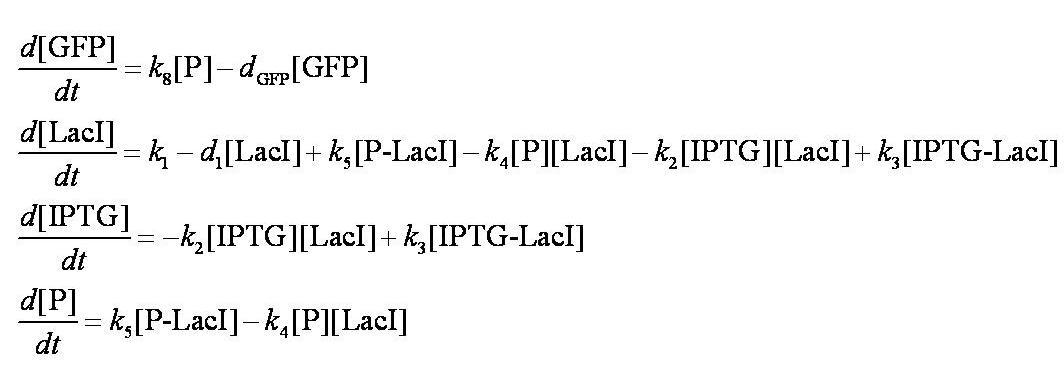Team:Imperial College/Genetic Circuit Details
From 2008.igem.org
| Line 43: | Line 43: | ||
====Equations==== | ====Equations==== | ||
| + | |||
| + | Before IPTG is introduced the system is in a steady state: | ||
| + | |||
| + | [[Image:Pre_IPTG_Steady_States_Complex_Model.jpg|400px]] | ||
| + | |||
| + | Note: k1 and k8 represent the rate of transcription through the constitutive promoter upstream of LacI and the promoter upstream of GFP respectively. | ||
| + | |||
| + | d1 and dGFP represent the degradation rates of LacI and GFP respectively. | ||
| + | |||
| + | k_beta is defined as k4/k5. | ||
| + | |||
| + | When IPTG is introduced, the dynamic behaviour of the system is described using a system of ODEs. | ||
====Qualitative effect of parameters on behaviour==== | ====Qualitative effect of parameters on behaviour==== | ||
Revision as of 00:34, 29 October 2008
|
|||||||||||||||
 "
"