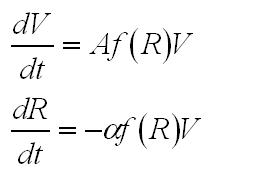Team:Imperial College/Growth Curve
From 2008.igem.org
| Line 52: | Line 52: | ||
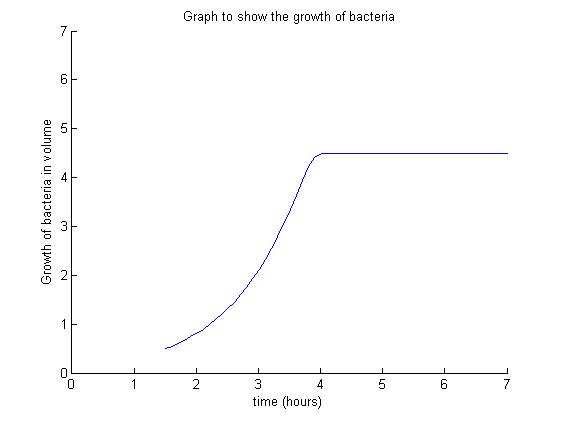
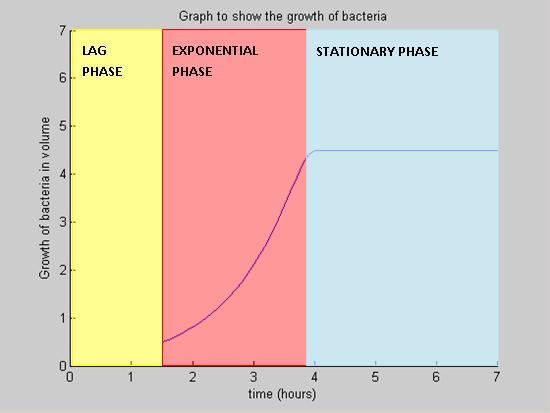
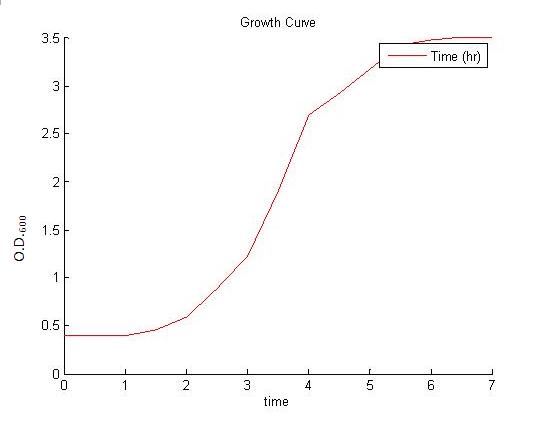
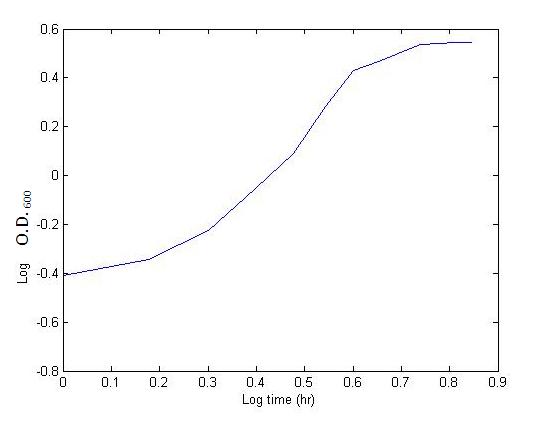
We chose to represent the growth in terms of overall volume rather than number of cells. | We chose to represent the growth in terms of overall volume rather than number of cells. | ||
| - | For small volumes (lag phase and early exponential phase) the volume is a smoother variable (the overall volume grows a little already in the lag phase) while at larger volume, the volume and the number of cells are proportional. | + | For small volumes (lag phase and early exponential phase) the volume is a smoother variable (the overall volume grows a little already in the lag phase) while at larger volume, the volume and the number of cells are proportional. <br> |
Considering the overall volume also regularises the process since it allows us, to some extent, to overlook the process of cell division during the bacteria growth. We can indeed assume the internal concentration of nutrients is reset almost instantaneously to the external concentration. During this time, the total volume does not change. | Considering the overall volume also regularises the process since it allows us, to some extent, to overlook the process of cell division during the bacteria growth. We can indeed assume the internal concentration of nutrients is reset almost instantaneously to the external concentration. During this time, the total volume does not change. | ||
| + | <br><br> | ||
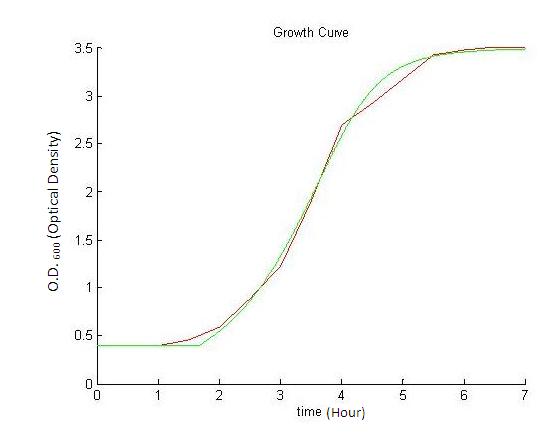
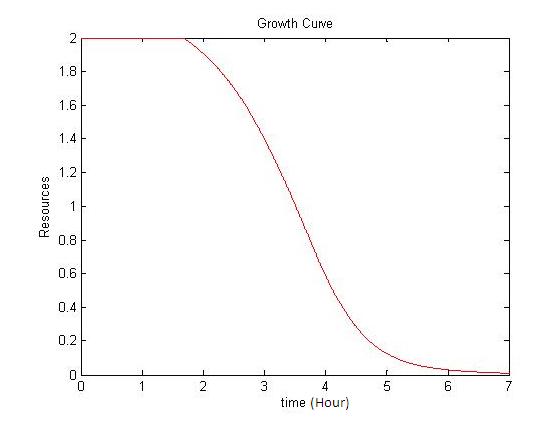
| + | In order to couple growth with resources, our model curbs the optimal growth rate of the volume (A) with a function f of the resources R. We used a Hill function of exponent n, as it models with only one parameter the fact that production is unhindered when resources are plentiful and minimal when resources have run out. | ||
| + | <br> | ||
| + | Finally we assume that in term of resources the cost of an extra unit of volume is alpha. | ||
| + | <br><br> | ||
The growth of the overall volume V is therefore modelled as: | The growth of the overall volume V is therefore modelled as: | ||
Revision as of 20:38, 29 October 2008
Modelling the Growth Curve
|
|||||||||||||||||
 "
"