Team:Edinburgh/Modelling/Kinetic
From 2008.igem.org
(→Ordinary Differential Equations) |
(→References) |
||
| (4 intermediate revisions not shown) | |||
| Line 12: | Line 12: | ||
Through mathematical modelling of cellular processes, we aim to reflect | Through mathematical modelling of cellular processes, we aim to reflect | ||
biological function in sets of equations supplied with parameter values | biological function in sets of equations supplied with parameter values | ||
| - | that best fit observed reality (Drillon, G. 2008). If the outcomes of modelled simulations closely correspond to experimental results, the model is valuable for understanding the biological mechanism. Thus through modelling we may generate new hypotheses at low cost, while also investigating and corroborating or ending doubts about previous hypotheses | + | that best fit observed reality (Drillon, G. 2008). If the outcomes of modelled simulations closely correspond to experimental results, the model is valuable for understanding the biological mechanism. Thus through modelling we may generate new hypotheses at low cost, while also investigating and corroborating or ending doubts about previous hypotheses (Baralla, 2008). Modelling in |
preparation and in response to wetlab work can save money and time by | preparation and in response to wetlab work can save money and time by | ||
focussing on more likely hypotheses. | focussing on more likely hypotheses. | ||
A standard way of modelling (non-spatial) physical systems which has been | A standard way of modelling (non-spatial) physical systems which has been | ||
| - | successfully applied to simulate metabolic systems | + | successfully applied to simulate metabolic systems (Bakker et al., 1997) is the use of |
Ordinary Differential Equations (ODEs). The aim of using ODEs is to describe a biological phenomenon, so that the time dynamics of the system can be analyzed or the steady state values of the variables involved in the model can be calculated. The effects of transcriptional regulation as well as of the changes in concentration of metabolites via enzymes are thus simulated. | Ordinary Differential Equations (ODEs). The aim of using ODEs is to describe a biological phenomenon, so that the time dynamics of the system can be analyzed or the steady state values of the variables involved in the model can be calculated. The effects of transcriptional regulation as well as of the changes in concentration of metabolites via enzymes are thus simulated. | ||
| Line 32: | Line 32: | ||
==The Model== | ==The Model== | ||
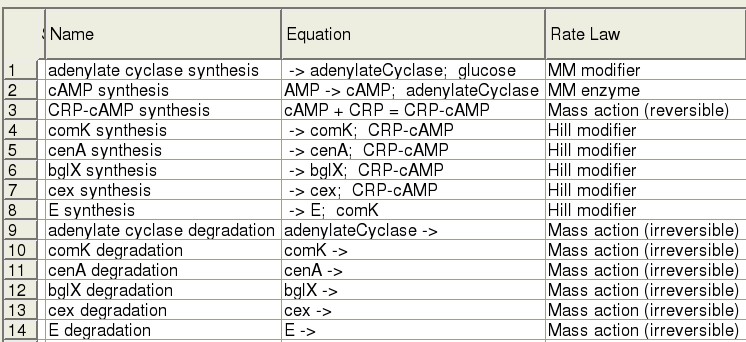
| - | + | Modelling was accomplished using [http://www.copasi.org/tiki-index.php COPASI]. Each step of the pathway is expressed using an appropriate rate law and short-hand reaction equation. | |
[[Image:Edinburgh-ModelTable.jpg]] | [[Image:Edinburgh-ModelTable.jpg]] | ||
| - | Our survey of the literature yielded some kinetic information for the genes in our system, in vivo, as well as in E. coli. Parameter values are currently being fit. | + | Our survey of the literature yielded some kinetic information for the genes in our system, in vivo, as well as in E. coli. Parameter values are currently being fit. |
| - | + | ||
==Ordinary Differential Equations== | ==Ordinary Differential Equations== | ||
| Line 44: | Line 43: | ||
[[Image:Edinburgh-ModelODEs.jpg]] | [[Image:Edinburgh-ModelODEs.jpg]] | ||
| + | |||
| + | |||
| + | ==References== | ||
| + | |||
| + | * Bakker, BM., Michelis, PAM., Opperdoes, FR, and Westerhoff, HV. (1997). Glycolysis in bloodstream from trypanasoma brucei can be understood in terms of the kinetics of the glycotic enzymes. ''J. Biol. Chem.'', '''272''':3207–3215. | ||
| + | |||
| + | * Baralla, A. (2008). ''Modeling and parameter estimation of the sos response network in E. coli''. Technical report, University of Trento. | ||
| + | |||
| + | * Drillon, G.(2008). MSc Thesis: ''An Integrated Kinetic Model of Ammonia Assimilation Regulation in Escherichia coli''. University of Edinburgh. | ||
Latest revision as of 04:08, 30 October 2008
Contents |
Introduction
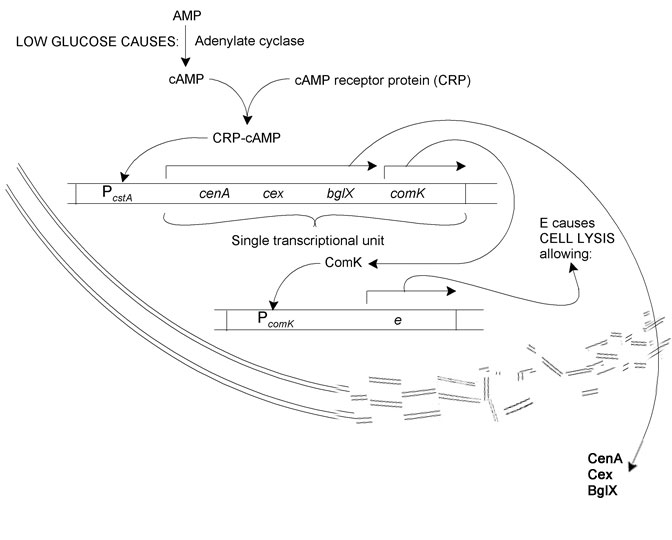
This section aims to outline the model of the cellulase secretion pathway for cellulose degradation as constructed by the University of Edinburgh 2008 iGEM team. The computational model includes two operons, 14 species, and 15 reactions, and focusses on the switching on of genes for cellulose degradation by CRP-cAMP.
Kinetic Modelling
Through mathematical modelling of cellular processes, we aim to reflect biological function in sets of equations supplied with parameter values that best fit observed reality (Drillon, G. 2008). If the outcomes of modelled simulations closely correspond to experimental results, the model is valuable for understanding the biological mechanism. Thus through modelling we may generate new hypotheses at low cost, while also investigating and corroborating or ending doubts about previous hypotheses (Baralla, 2008). Modelling in preparation and in response to wetlab work can save money and time by focussing on more likely hypotheses.
A standard way of modelling (non-spatial) physical systems which has been successfully applied to simulate metabolic systems (Bakker et al., 1997) is the use of Ordinary Differential Equations (ODEs). The aim of using ODEs is to describe a biological phenomenon, so that the time dynamics of the system can be analyzed or the steady state values of the variables involved in the model can be calculated. The effects of transcriptional regulation as well as of the changes in concentration of metabolites via enzymes are thus simulated.
The Biological System
The system we sought to model is as follows: Reduction in glucose concentration leads to increased adenylate cyclase activity. This results in more AMP being converted to cAMP. cAMP binds to CRP. The resultant CRP-cAMP transcription factor activates the transcription of cellulase and cellubiase proteins (cenA, cex, and bglX) and comK via the cstA operator. ComK in turn binds to the comK operator, whereupon phiX174E, a lysis enzyme, is produced. Cell lysis releases the cellulases and bglX into the growth medium.
The Model
Modelling was accomplished using [http://www.copasi.org/tiki-index.php COPASI]. Each step of the pathway is expressed using an appropriate rate law and short-hand reaction equation.
Our survey of the literature yielded some kinetic information for the genes in our system, in vivo, as well as in E. coli. Parameter values are currently being fit.
Ordinary Differential Equations
ODEs of the kinetic model as generated by the COPASI modelling application.
References
- Bakker, BM., Michelis, PAM., Opperdoes, FR, and Westerhoff, HV. (1997). Glycolysis in bloodstream from trypanasoma brucei can be understood in terms of the kinetics of the glycotic enzymes. J. Biol. Chem., 272:3207–3215.
- Baralla, A. (2008). Modeling and parameter estimation of the sos response network in E. coli. Technical report, University of Trento.
- Drillon, G.(2008). MSc Thesis: An Integrated Kinetic Model of Ammonia Assimilation Regulation in Escherichia coli. University of Edinburgh.
 "
"