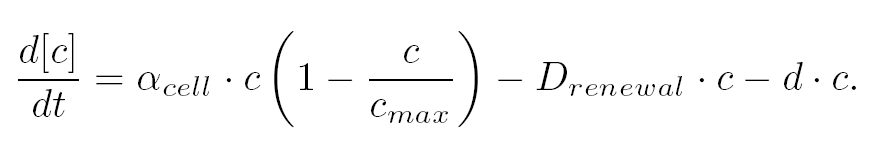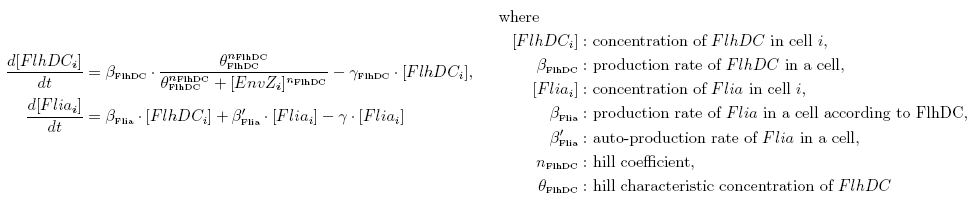Team:Paris/DescriptionDetailsS4-S2Part1
From 2008.igem.org
(Difference between revisions)
| (One intermediate revision not shown) | |||
| Line 1: | Line 1: | ||
| - | |||
| - | |||
| - | |||
{| | {| | ||
|-style="background: #649CD7; text-align: center;" | |-style="background: #649CD7; text-align: center;" | ||
| Line 10: | Line 7: | ||
|[[Image:final_chemostat.png|center|300px]] | |[[Image:final_chemostat.png|center|300px]] | ||
|-style="background: #ffffff; text-align: left;" | |-style="background: #ffffff; text-align: left;" | ||
| - | | For the production term, we use a logistic equation to model cell growth, according to standard assumptions. The | + | | For the production term, we use a logistic equation to model cell growth, according to standard assumptions. The behaviour obtained is the following one: at low population density, the concentration of cells in the chemostat (c) increase exponentially with a growth rate α<sub>cell</sub> and at high population density, the population reaches a maximum concentration, c<sub>max</sub>. |
|-style="background: #ffffff; text-align: left;" | |-style="background: #ffffff; text-align: left;" | ||
| - | | For the degradation term, we consider that c decrease | + | | For the degradation term, we consider that c decrease proportionally to both a dilution phenomena cause by the renewal of the medium in the chemostat (D<sub>renewal</sub>) and cell death (d). |
|-style="background: #649CD7; text-align: center;" | |-style="background: #649CD7; text-align: center;" | ||
|Common Dynamics: Quorum Sensing | |Common Dynamics: Quorum Sensing | ||
| Line 18: | Line 15: | ||
|In order to model the quorum sensing dynamics, we consider that: | |In order to model the quorum sensing dynamics, we consider that: | ||
|-style="background: #ffffff; text-align: left;" | |-style="background: #ffffff; text-align: left;" | ||
| - | | 1) Inside a cell, the HSL concentration increases | + | | 1) Inside a cell, the HSL concentration increases proportionally to the concentration of LasI and decreases according to both a degradation term (proportional to the internal HSL concentration) and a transport term (proportional to the difference between the internal and external concentration of HSL). Thus, the equation for the internal HSL concentration is: |
|-style="background: #ffffff; text-align: center;" | |-style="background: #ffffff; text-align: center;" | ||
|[[Image:final_HSL.png|center|400px|]] | |[[Image:final_HSL.png|center|400px|]] | ||
|-style="background: #ffffff; text-align: left;" | |-style="background: #ffffff; text-align: left;" | ||
| - | | 2) Outside the cells, HSL is | + | | 2) Outside the cells, HSL is accumulated with the same transport term that we use in the previous equation. The degradation of HSL in the external medium and the dilution controlled via the chemostat accounts for HSL external decrease. So the external HSL concentration is given by: |
|-style="background: #ffffff; text-align: left;" | |-style="background: #ffffff; text-align: left;" | ||
|[[Image:HSLext.png|center|350px]] | |[[Image:HSLext.png|center|350px]] | ||
| Line 37: | Line 34: | ||
|-style="background: #ffffff; text-align: center;" | |-style="background: #ffffff; text-align: center;" | ||
|[[Image:FlhDC-FliaEq.png|650px]] | |[[Image:FlhDC-FliaEq.png|650px]] | ||
| - | |||
|} | |} | ||
 "
"