Team:Imperial College/Genetic Circuit
From 2008.igem.org
m (Small grammar edits) |
|||
| (23 intermediate revisions not shown) | |||
| Line 3: | Line 3: | ||
=== Modelling the Genetic Circuit === | === Modelling the Genetic Circuit === | ||
{{Imperial/Box2|| | {{Imperial/Box2|| | ||
| - | An accurate mathematical description of the behaviour of | + | An accurate mathematical description of the behaviour of genetic circuits is essential for projects involving synthetic biology. Such descriptions are an integral component of part submission to the Registry, as exemplified by the canonical characterisation of part F2620 ({{ref|1}}). The ability to capture part behaviour as a mathematical relationship between input and output is useful for future re-use of the part and modification or integration into novel genetic circuits.}} |
{{Imperial/Box1|Modelling Constitutive Gene Expression| | {{Imperial/Box1|Modelling Constitutive Gene Expression| | ||
| - | + | A simple <html><a target="_blank" href="http://openwetware.org/wiki/Imperial_College/Courses/Spring2008/Synthetic_Biology/Computer_Modelling_Practicals/Practical_2">synthesis-degradation model</a></html> is assumed for the modelling of the expression of a protein under the control of a constitutive promoter, with the same model assumed for all four [[Team:Imperial_College/Cloning_Strategy | promoter-RBS constructs]]. The synthesis-degradation model assumes a steady state level of mRNA. | |
| - | A simple | + | |
[[Image:Eq1.png]] | [[Image:Eq1.png]] | ||
| - | In this case, [protein] represents the concentration of GFP, which will be the reporter protein in our constructs used for | + | In this case, [protein] represents the concentration of GFP, which will be the reporter protein in our constructs used for characterization. k<sub>1</sub> represents the rate of synthesis and d<sub>1</sub> represents the degradation rate. |
| - | We can easily simulate this synthesis-degradation model using Matlab; the ODEs and simulation file can be found in the | + | We can easily simulate this synthesis-degradation model using Matlab; the ODEs and simulation file can be found in the dry lab appendices. |
| - | + | ||
| - | + | ||
We can also solve this ODE analytically. | We can also solve this ODE analytically. | ||
| Line 27: | Line 24: | ||
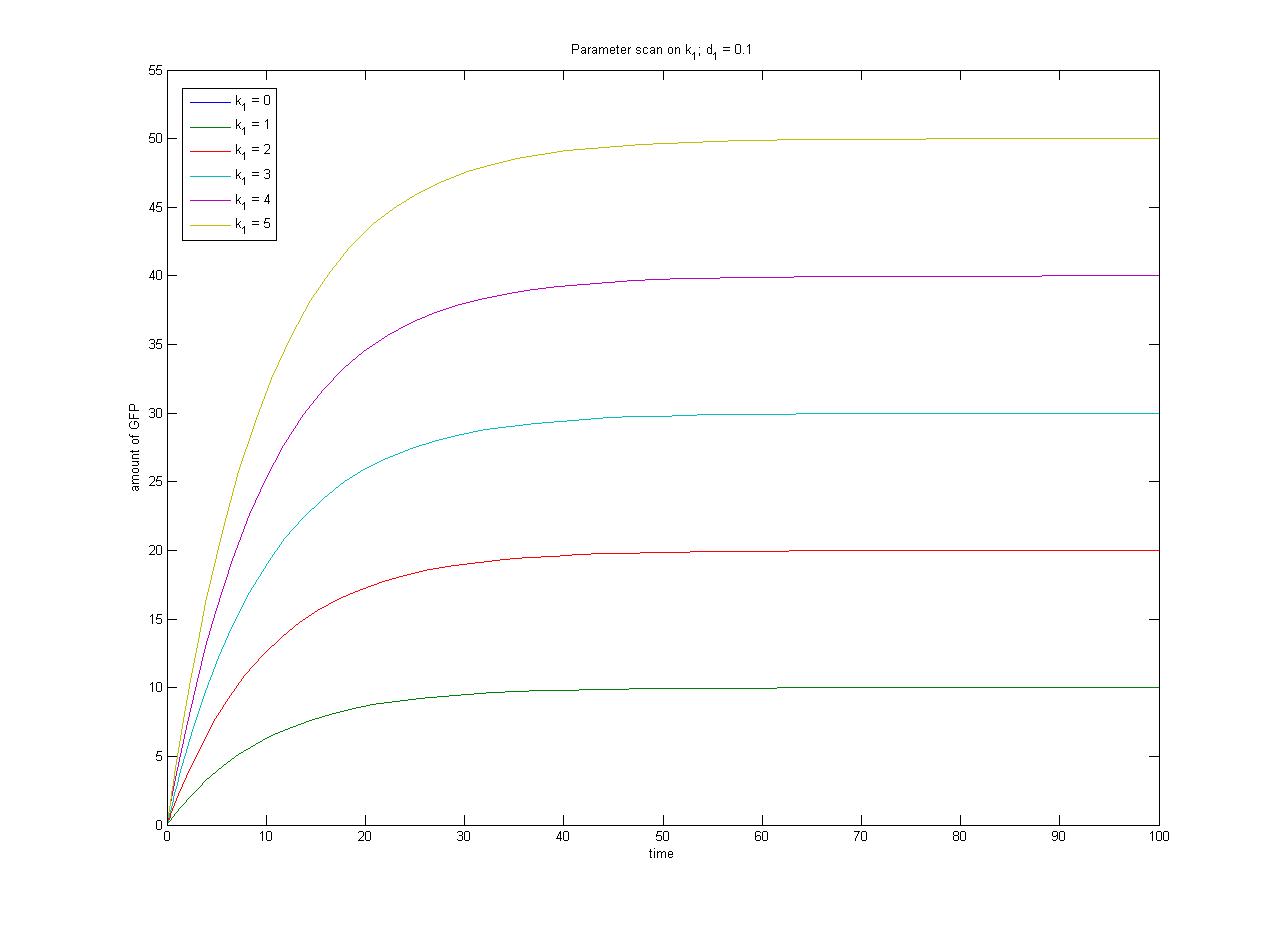
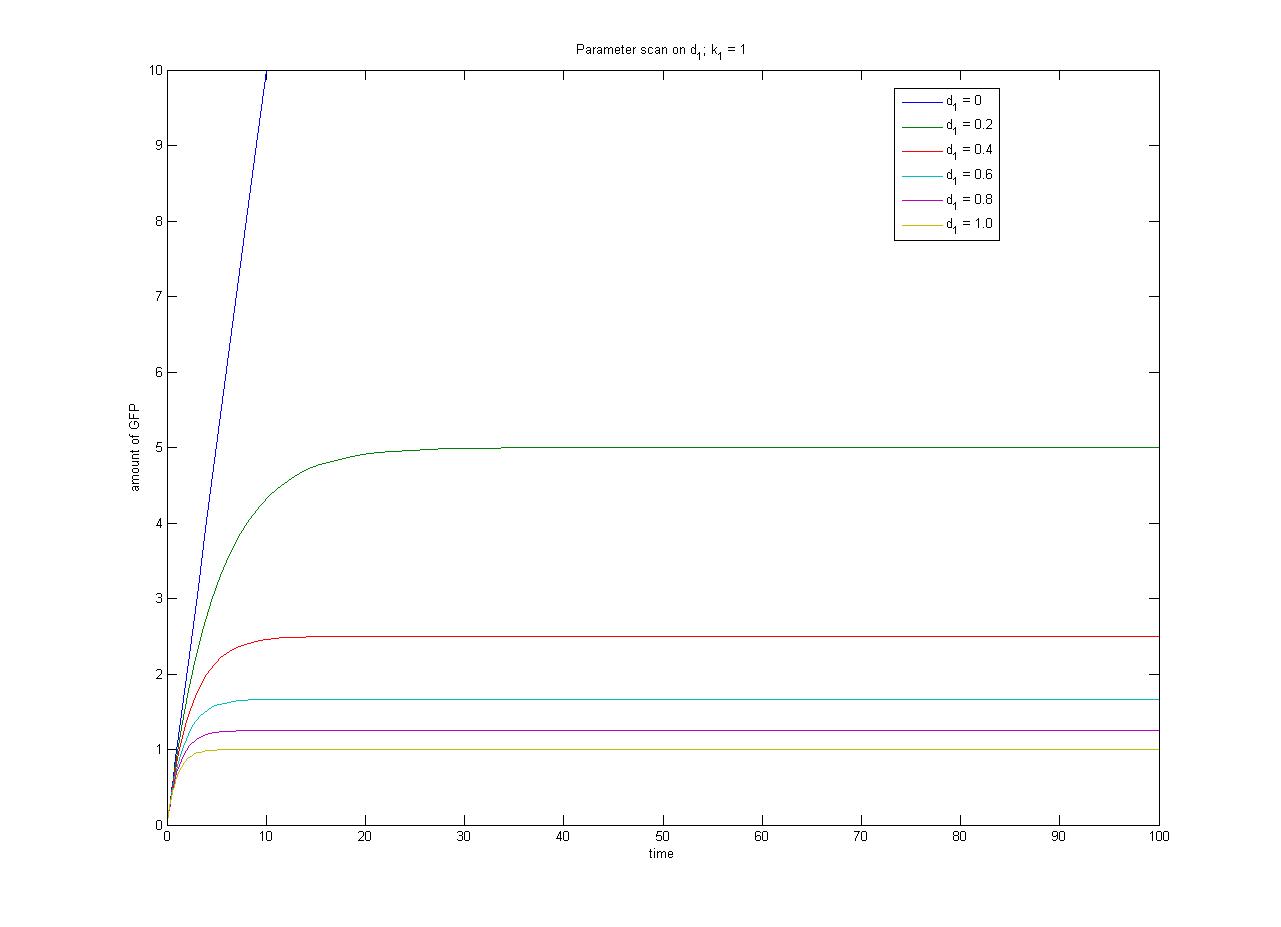
Note from the parameter scan graphs:<br> | Note from the parameter scan graphs:<br> | ||
| - | *In the case where | + | *In the case where k<sub>1</sub> {{Equals}} 0, no GFP is sythesised. |
| - | *In the case where | + | *In the case where d<sub>1</sub> {{Equals}} 0, the concentration of protein does not reach a steady state. |
From the wetlab experiments it is likely that we will obtain steady-state data for each of the four promoter-RBS constructs. If we assume the same rate of degradation of GFP in each case, we can use the relative steady-state levels of GFP as a proxy for the relative rate of transcription through each promoter. This will help us with the selection of the most appropriate promoter to use for Phase 2. In order to obtain an absolute measure of transcription (as opposed to a relative measure of transcriptional strength) we require constitutive expression in terms of molecules per cell (as opposed to fluorescence in arbitrary units). | From the wetlab experiments it is likely that we will obtain steady-state data for each of the four promoter-RBS constructs. If we assume the same rate of degradation of GFP in each case, we can use the relative steady-state levels of GFP as a proxy for the relative rate of transcription through each promoter. This will help us with the selection of the most appropriate promoter to use for Phase 2. In order to obtain an absolute measure of transcription (as opposed to a relative measure of transcriptional strength) we require constitutive expression in terms of molecules per cell (as opposed to fluorescence in arbitrary units). | ||
Complementary experiments to estimate the rate of degradation of GFP - by terminating transcription - would allow us to estimate absolute rate of transcription through each promoter. | Complementary experiments to estimate the rate of degradation of GFP - by terminating transcription - would allow us to estimate absolute rate of transcription through each promoter. | ||
| - | |||
| - | |[[Image:Phase 1.PNG|thumb| | + | |[[Image:Phase 1.PNG|thumb|300px|Constitutive expression of antibiotic resistance (AB) and GFP. GFP brick is part E0040, GFPmut3b. Terminator is part B0015, the double-stop.]] |
| - | [[Image:ParamterScanGFPk1.jpg| | + | [[Image:ParamterScanGFPk1.jpg|thumb|300px|Parameter scan on k<sub>1</sub>]] |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | [[ | + | [[Image:ParamterScanGFPd1.jpg|thumb|300px|Parameter scan on d<sub>1</sub>]] |
}} | }} | ||
{{Imperial/Box1|Two models of IPTG-induced expression of GFP under the control of the Plac promoter| | {{Imperial/Box1|Two models of IPTG-induced expression of GFP under the control of the Plac promoter| | ||
| - | |||
A literature search revealed two models of IPTG-induced expression through the Plac promoter. Both models assume constitutive expression of LacI. Before IPTG is added, a steady-state is reached comprising basal (leaky) expression of GFP. | A literature search revealed two models of IPTG-induced expression through the Plac promoter. Both models assume constitutive expression of LacI. Before IPTG is added, a steady-state is reached comprising basal (leaky) expression of GFP. | ||
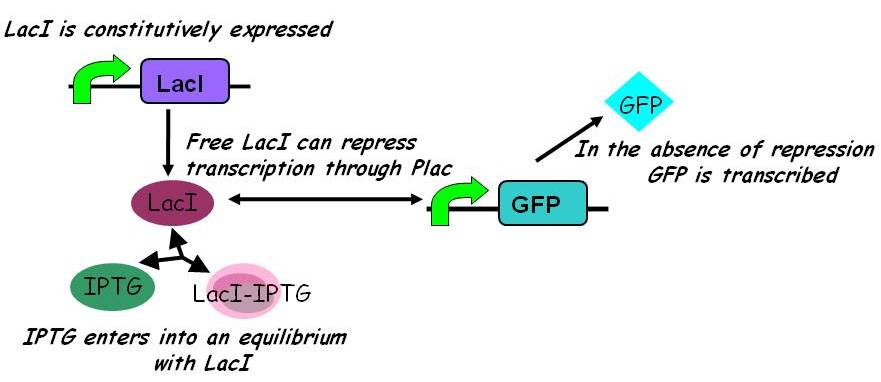
| - | In the simpler model ({{ref|2}}) IPTG competes with free promoter for LacI binding, but does not itself bind to the LacI-promoter complex. | + | ====== Simpler model ====== |
| + | In the simpler model ({{ref|2}}) IPTG competes with free promoter for LacI binding, but does not itself bind to the LacI-promoter complex. | ||
| - | [[ | + | [[Team:Imperial_College:Genetic_Circuit_Details_2 |'''>>> Details >>>''']] |
| - | + | [[Image:Igem2008 - inducible promoters.jpg|435px]] | |
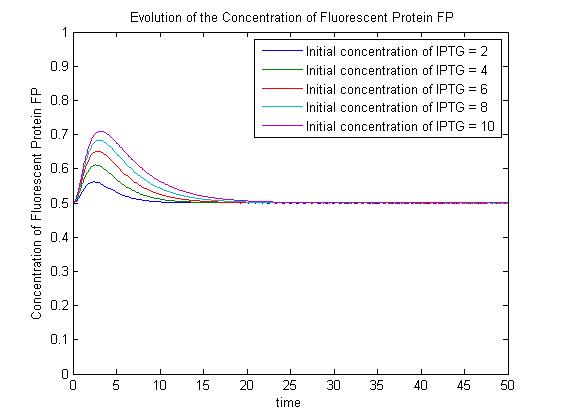
| - | + | Under this model, with all other parameters constant, the steady-state concentration of free promoter and hence the steady-state concentration of GFP are independent of the initial concentration of IPTG. (See time evolution of GFP expression assuming different concentrations of IPTG are used for induction, right.) | |
| - | + | ||
The pre-steady-state dynamic behaviour of the GFP concentration will differ with different initial concentrations of IPTG (but the steady-state behaviour will not). Hence, accurate data collection during the pre-steady-state phase is crucial for parameter estimation. | The pre-steady-state dynamic behaviour of the GFP concentration will differ with different initial concentrations of IPTG (but the steady-state behaviour will not). Hence, accurate data collection during the pre-steady-state phase is crucial for parameter estimation. | ||
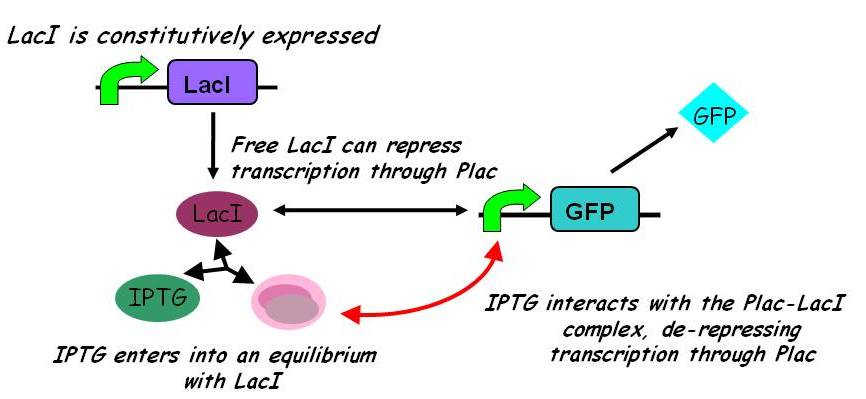
| + | ====== More complex model ====== | ||
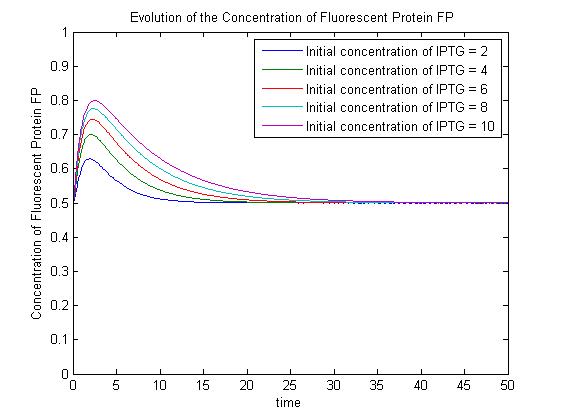
A more sophisticated model allows for interaction between IPTG and the promoter-LacI complex ({{ref|3}}). IPTG can bind to the promoter-LacI complex to form IPTG-LacI and free promoter. This eases the repression by LacI and allows transcription of GFP. | A more sophisticated model allows for interaction between IPTG and the promoter-LacI complex ({{ref|3}}). IPTG can bind to the promoter-LacI complex to form IPTG-LacI and free promoter. This eases the repression by LacI and allows transcription of GFP. | ||
| - | [[Image:Inducible_promoters_2.jpg| | + | [[Image:Inducible_promoters_2.jpg|435px]] |
| - | Under this model, the dynamic behaviour (whether or not [GFP] attains a maximum higher than its steady-state value) depends on the relative strengths of the kinetic constants describing the interactions underlying the model. Either way, | + | Under this model, the dynamic behaviour (whether or not [GFP] attains a maximum higher than its steady-state value) depends on the relative strengths of the kinetic constants describing the interactions underlying the model. Either way, the steady-state [GFP] will vary as a Hill-function dependent on the initial concentration of IPTG; this characteristic can be used to discriminate between the two models. |
| - | + | ODEs and simulation m-files for further exploration of the properties of these models can, again, be found in the appendices. | |
| - | + | ||
[[Team:Imperial_College/Genetic_Circuit_Details | '''>>> Details of equilibria and equations and qualitative discussion of parameter effects >>>''']] | [[Team:Imperial_College/Genetic_Circuit_Details | '''>>> Details of equilibria and equations and qualitative discussion of parameter effects >>>''']] | ||
| - | |[[Image:SimpleModel_2.jpg|thumb|300px|Pre-steady-state time evolution of GFP using the simple model.]]<br>[[Image:ComplexModel3.jpg|thumb| | + | |[[Image:SimpleModel_2.jpg|thumb|300px|Pre-steady-state time evolution of GFP using the simple model.]]<br>[[Image:ComplexModel3.jpg|thumb|300px|Pre-steady-state time evolution of GFP using the more sophisticated model.]]}} |
{{Imperial/Box2|| | {{Imperial/Box2|| | ||
===== References ===== | ===== References ===== | ||
#{{FormatRef|Canton B, Labno A, & Endy D|2008|Refinement and standardization of synthetic biological parts and devices.|Nature biotechnology 26 (7)|787-793|}} | #{{FormatRef|Canton B, Labno A, & Endy D|2008|Refinement and standardization of synthetic biological parts and devices.|Nature biotechnology 26 (7)|787-793|}} | ||
| - | |||
#{{FormatRef|Alon, U|2006|An Introduction to Systems Biology: Design Principles of Biological Circuits|||Chapman & Hall/Crc Mathematical and Computational Biology}} | #{{FormatRef|Alon, U|2006|An Introduction to Systems Biology: Design Principles of Biological Circuits|||Chapman & Hall/Crc Mathematical and Computational Biology}} | ||
| + | #{{FormatRef|Kuhlman T, Zhang Z, Saier MH Jr, & Hwa T|2007|Combinatorial transcriptional control of the lactose operon of Escherichia coli.|PNAS 104 (14)|6043-6048|}} | ||
|}} | |}} | ||
{{Imperial/EndPage|Growth_Curve|Motility}} | {{Imperial/EndPage|Growth_Curve|Motility}} | ||
Latest revision as of 04:03, 27 July 2009
Modelling the Genetic Circuit
|
|||||||||||||||||||
 "
"