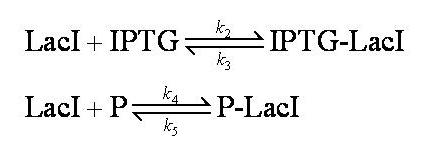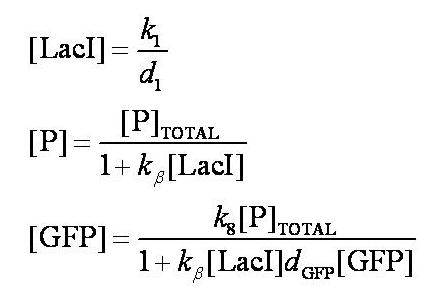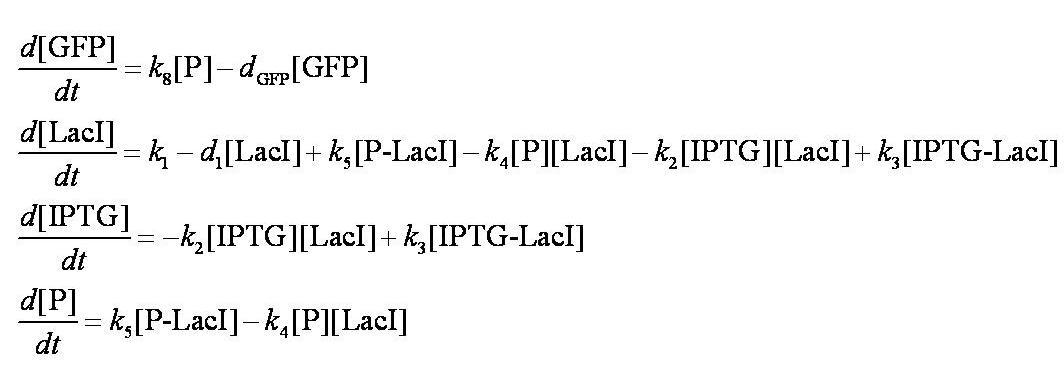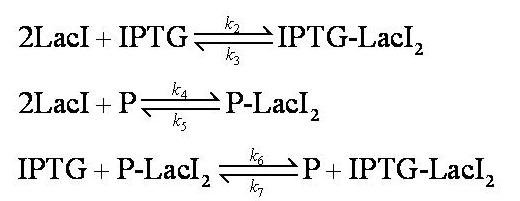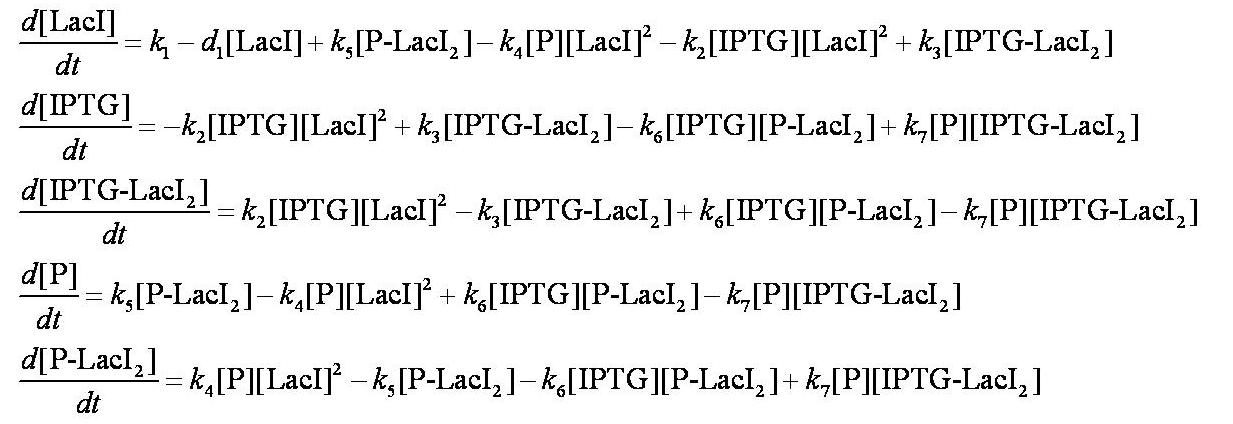Team:Imperial College/Genetic Circuit Details
From 2008.igem.org
m |
|||
| (6 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{Imperial/StartPage2}} | {{Imperial/StartPage2}} | ||
| - | {{Imperial/Box1|Simple Model ({{ref|1}}) | | + | {{Imperial/Box1|Simple Model ({{ref|1}})| |
| - | ====Equilibria==== | + | [[Image:Igem2008_-_inducible_promoters.jpg|450px]] |
| + | ====== Equilibria ====== | ||
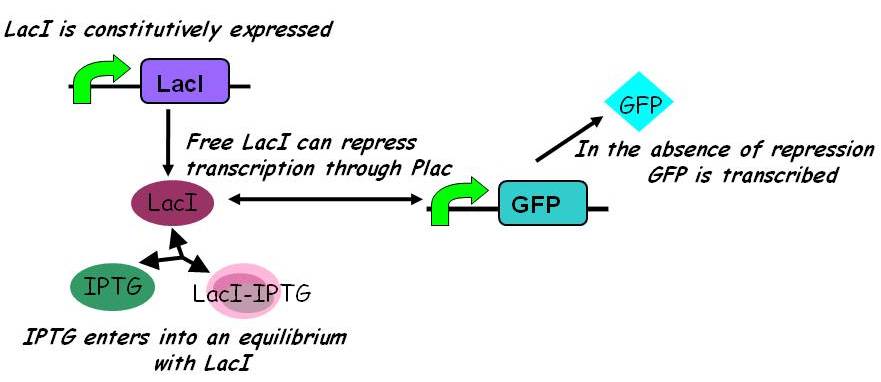
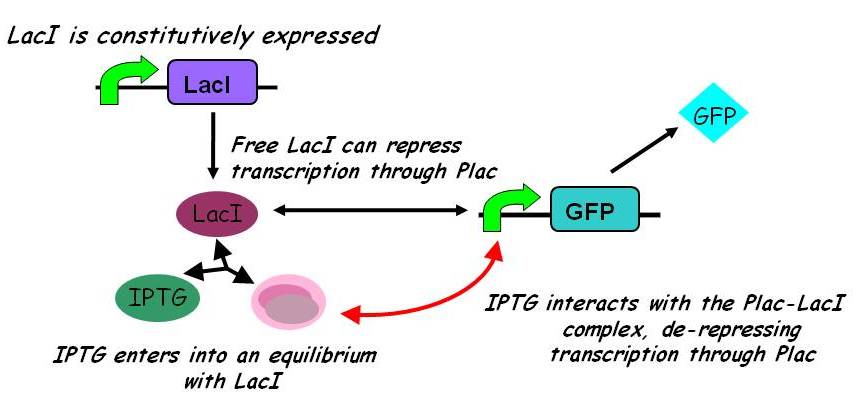
Interactions between IPTG, LacI and free promoter and the formation of the promoter-LacI and IPTG-LacI complexes are described using the following equilibria. | Interactions between IPTG, LacI and free promoter and the formation of the promoter-LacI and IPTG-LacI complexes are described using the following equilibria. | ||
| - | [[Image:Simple_model_equilibria.jpg| | + | [[Image:Simple_model_equilibria.jpg|350px]] |
Note: 1:1 stoichiometry has been assumed; this model could be adapted to use different stoichiometric coefficients. | Note: 1:1 stoichiometry has been assumed; this model could be adapted to use different stoichiometric coefficients. | ||
k<sub>2</sub>, k<sub>3</sub>, k<sub>4</sub> and k<sub>5</sub> represent binding constants for formation and dissociation of complexes. | k<sub>2</sub>, k<sub>3</sub>, k<sub>4</sub> and k<sub>5</sub> represent binding constants for formation and dissociation of complexes. | ||
| - | ====Equations==== | + | ====== Equations ====== |
Before IPTG is introduced the system is at steady-state. The steady-state levels of LacI, free promoter, and GFP are given by: | Before IPTG is introduced the system is at steady-state. The steady-state levels of LacI, free promoter, and GFP are given by: | ||
| Line 23: | Line 24: | ||
To describe the change in concentration of the interacting species over time we used the following system of differential equations: | To describe the change in concentration of the interacting species over time we used the following system of differential equations: | ||
| - | [[Image:Simple_model_ODEs.jpg| | + | [[Image:Simple_model_ODEs.jpg|700px]] |
These are evaluated numerically using Matlab's ODE solver. | These are evaluated numerically using Matlab's ODE solver. | ||
| Line 30: | Line 31: | ||
}} | }} | ||
| - | {{Imperial/Box1|More Sophisticated Model({{ref|2}})| | + | {{Imperial/Box1|More Sophisticated Model ({{ref|2}})| |
| - | ====Equilibria==== | + | [[Image:Inducible_promoters_2.jpg|450px]] |
| - | [[Image:Complex_model_equilibria.jpg| | + | ====== Equilibria ====== |
| + | [[Image:Complex_model_equilibria.jpg|350px]] | ||
Assumptions: | Assumptions: | ||
| Line 42: | Line 44: | ||
Note: k<sub>2</sub>, k<sub>3</sub>, k<sub>4</sub>, k<sub>5</sub>, k<sub>6</sub> and k<sub>7</sub> represent binding constants for formation and dissociation of complexes. | Note: k<sub>2</sub>, k<sub>3</sub>, k<sub>4</sub>, k<sub>5</sub>, k<sub>6</sub> and k<sub>7</sub> represent binding constants for formation and dissociation of complexes. | ||
| - | ====Equations==== | + | ====== Equations ====== |
Before IPTG is introduced the system is in a steady state: | Before IPTG is introduced the system is in a steady state: | ||
| Line 56: | Line 58: | ||
When IPTG is introduced, the dynamic behaviour of the system is described using a system of ODEs. | When IPTG is introduced, the dynamic behaviour of the system is described using a system of ODEs. | ||
| - | [[Image:Complex_Model_ODEs.jpg| | + | [[Image:Complex_Model_ODEs.jpg|750px]] |
These are evaluated numerically using Matlab's ODE solver. | These are evaluated numerically using Matlab's ODE solver. | ||
| - | ====Qualitative effect of parameters on behaviour==== | + | ====== Qualitative effect of parameters on behaviour ====== |
Two different regimes of behaviour can be exhibited by the concentration of GFP over time as described by the more complex model, dependent on the parameters defining the ODE system. | Two different regimes of behaviour can be exhibited by the concentration of GFP over time as described by the more complex model, dependent on the parameters defining the ODE system. | ||
Latest revision as of 02:50, 30 October 2008
|
|||||||||||||||
 "
"