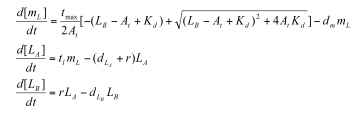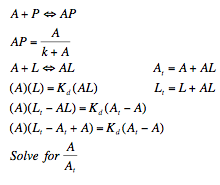Team:Michigan/Project/Modeling/Model1.html
From 2008.igem.org
| (20 intermediate revisions not shown) | |||
| Line 9: | Line 9: | ||
= '''<font color=dodgerblue size=6>Sequestillator Model 1: A simple model</font>''' = | = '''<font color=dodgerblue size=6>Sequestillator Model 1: A simple model</font>''' = | ||
| + | <div align='center'>[[Image:Model1Equations.png]] [[Image:Derivation.png]]</div> | ||
| + | Parameters: | ||
| + | *At= total amount of NifA | ||
| + | *tmax= maximal transcription rate | ||
| + | *tl=translation rate | ||
| + | *r = conversion rate from La to Lb | ||
| + | *Kd= dissociation constant of NifL and Nifa (= kr/kf, where kf is the forward binding rate of NifL and NifA and kr is the rate of decomposition of the NifL/NifA complex) | ||
| + | *any d= degradation rate of that species | ||
| + | Professor Daniel Forger came up with this model for the Sequestillator. This simple system assumes the total amount of NifA in the system is constant, and considers three variable: NifL mRNA (mL), NifL (La), and a simple covalent modification of NifL (Lb). The quadratic mRNA production function comes from making rapid equilibrium assumptions (see box to the right of the equations. A= free unbound NifA, L = unbound NifL). From analyzing this small model, we were able to see that in order for oscillations to exist, there needed to be a tight binding between NifL and NifA (i.e., Kd is very small) and one-to-one titration of NifL and NifA (the mRNA production function = tmax*A/At, where A is free NifA in the system. A graph of the function vs. Lb is a oblique line). | ||
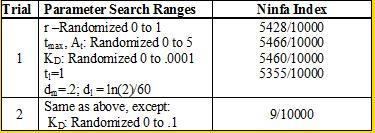
| + | <br> We used the Indexilator to make some "relative" Ninfa index searches. Look at table 1 below: | ||
| + | <div align='center'>[[Image:chart.png]]<br> | ||
| + | <b>Table 1</b><br></div> | ||
| + | We see that if we increase our search range for the dissociation constant to 0 to .1, then we get a substantially smaller Ninfa index, illustrating the importance of having a tight binding between NifA and NifL. | ||
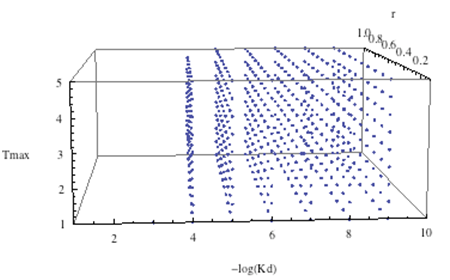
| + | <br> Some "sequential" searches (i.e., instead of randomizing, we picked incremental values for each parameters: i.e., one parameter would be varied from 1 to 10 in increments of 1, and another from 1 to 5 in increments of .5. Given below is a three-dimensional cloud picture, of -log(Kd)vs At vs tmax.: | ||
| + | <div align='center'>[[Image:cloud.png]]<br> | ||
| + | <b>Picture 1</b><br></div> | ||
| + | <br> -log(Kd) was tested at values 1 to 10 in increments of 1 (for some reason, the -log(Kd)=10 values got cut off). Tmax was ranged from 0 to 5 in .2 increments, and r was ranged from 0 to 1 in .1 increments. Each dot in the plot corresponds to a set of parameters that gave oscillations. Notice that for -log(Kd)= 2 or 1, we see no oscillations at all - this yet another testament to necessity to have a small Kd in order for oscillations to occur. | ||
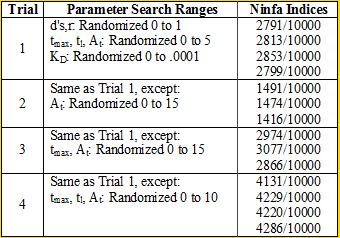
| - | + | There was another aspect of our model that we can also verify: the importance of a one-to-one NifA/NifL titration: | |
| - | + | <div align='center'>[[Image:chart2.png]]<br> | |
| - | <div align='center'>[[Image: | + | |
| - | + | ||
| - | + | ||
<b>Table 2</b> <br></div> | <b>Table 2</b> <br></div> | ||
| + | We see in trial 2, by increasing the range of At to 0 to 15 (and hence increasing the chance of having larger values of At), we have a reduction in the Ninfa index, as the system is unbalanced (too much At around). We return to similar Trial 1 results when we also vary tmax between 0 to 15 in Trial 3. | ||
| + | |||
| + | FURTHER WORK THAT WILL BE PRESENTED DURING iGEM POSTER TALKS | ||
| + | *More simulations; search over larger regions of parameter space. | ||
| + | *A more continuous cloud picture - the one given here has too much empty space.... | ||
| + | <br> [https://2008.igem.org/Team:Michigan/Project/Modeling Back to Modeling Main] | ||
|} | |} | ||
Latest revision as of 01:36, 30 October 2008
|
|---|
|
Sequestillator Model 1: A simple modelParameters:
Professor Daniel Forger came up with this model for the Sequestillator. This simple system assumes the total amount of NifA in the system is constant, and considers three variable: NifL mRNA (mL), NifL (La), and a simple covalent modification of NifL (Lb). The quadratic mRNA production function comes from making rapid equilibrium assumptions (see box to the right of the equations. A= free unbound NifA, L = unbound NifL). From analyzing this small model, we were able to see that in order for oscillations to exist, there needed to be a tight binding between NifL and NifA (i.e., Kd is very small) and one-to-one titration of NifL and NifA (the mRNA production function = tmax*A/At, where A is free NifA in the system. A graph of the function vs. Lb is a oblique line).
We see that if we increase our search range for the dissociation constant to 0 to .1, then we get a substantially smaller Ninfa index, illustrating the importance of having a tight binding between NifA and NifL.
There was another aspect of our model that we can also verify: the importance of a one-to-one NifA/NifL titration: We see in trial 2, by increasing the range of At to 0 to 15 (and hence increasing the chance of having larger values of At), we have a reduction in the Ninfa index, as the system is unbalanced (too much At around). We return to similar Trial 1 results when we also vary tmax between 0 to 15 in Trial 3. FURTHER WORK THAT WILL BE PRESENTED DURING iGEM POSTER TALKS
|
|---|
 "
"