Team:Groningen/Modeling
From 2008.igem.org
(→Spatial Model) |
(→Spatial Model) |
||
| Line 15: | Line 15: | ||
When we run our model with default parameters, most closely resembling the parameters found in other publications we get the result shown below. In this image we can clearly see that cells that are close (too close) to the sender cell, are turned of (having too many neighbours) as well as the cells that are too far from the sender (having too few neighbours). | When we run our model with default parameters, most closely resembling the parameters found in other publications we get the result shown below. In this image we can clearly see that cells that are close (too close) to the sender cell, are turned of (having too many neighbours) as well as the cells that are too far from the sender (having too few neighbours). | ||
| - | [[Image:Rug.Band_prod1_0_001.png]] | + | [[Image:Rug.Band_prod1_0_001.png]][[Image:Band_prod1_0_001_2s.png]] |
==''Modeling''== | ==''Modeling''== | ||
Revision as of 17:54, 11 October 2008
Modelling
To gain insight into the working of our designs we try to develop reliable and realistic models. In our project we took two different approaches: an elaborate single-cell model and a 'higher level' spatial model. In the sections below we will give a summary of the findings concerning our models, for more details we refer to our full report.
Single Cell Model
Spatial Model
In order to create a spatial model of our system we simplified the single-cell model using Hill-equations, in these equations several reactions are combined into a single Ordinary Differential Equation. As an example consider a Lux inducible promoter which is followed by the GFP gene; in our single-cell model we would have a separate equation for each reaction taking place whereas in our spatial model this would be represented as a single equation that gives the production of GFP as a function of the amount of Lux present.
We this approach we ended up with a single ODE for each species (HSL, HSL:luxR, luxR, cI and GFP), these formula were were then solved using MATLAB's ode15s solver.
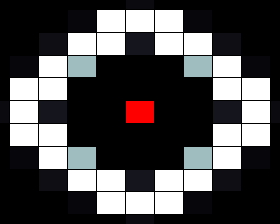
In our spatial model we used a grid where each cell is connected to four neighbours (left, right, top and bottom), with HSL diffusing freely to and from each connected cell according to a certain diffusion constant. In the resulting images, taken after giving the system enough time to reach a stable state, the red cells depict sender cells, which produce a constant amount of HSL, the white cells represent cells in the 'ON' state, and black cells depict cells in the 'OFF' state.
When we run our model with default parameters, most closely resembling the parameters found in other publications we get the result shown below. In this image we can clearly see that cells that are close (too close) to the sender cell, are turned of (having too many neighbours) as well as the cells that are too far from the sender (having too few neighbours).
Modeling
To gain insight into the working of our designs we try to develop reliable and realistic models.
The ODE solvers incorporated in the SimBiology package, for Mathworks' Matlab, are employed to model the genetic design on the single-cell level, displaying the variations in concentration of all relevant substances over time.
To examine the workings of our designs on the multi-cell level we are developing a routine in Matlab which can predict the collective behaviour of the designed cells on a two-dimensional grid. Hopefully this will help us to predict better the characteristics of HSL exchange between the cells.
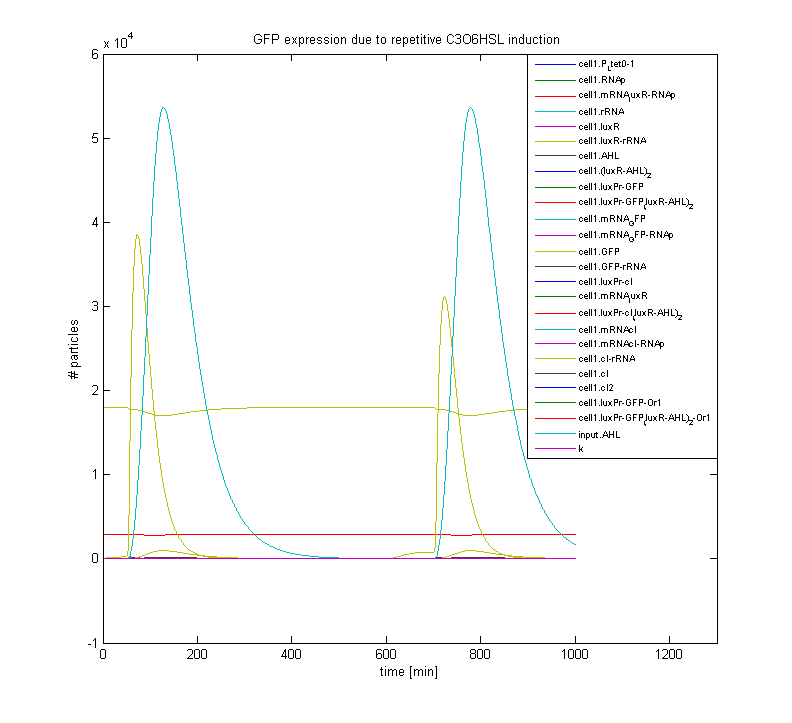
The figure below displays the response of a gene regulatory network, which incorporates an HSL sensing mechanism and a GFP reporter gene. Shown is the pulse-shaped GFP expression as a response to HSL induction; after induction the system relaxes towards its initial state, which makes it susceptible to repetitive stimuli.
 "
"