Team:Imperial College/Genetic Circuit
From 2008.igem.org
| Line 60: | Line 60: | ||
A literature search revealed two models of IPTG-induced expression through the Plac promoter. | A literature search revealed two models of IPTG-induced expression through the Plac promoter. | ||
| - | In the simpler model {{ref|2}} IPTG competes with free promoter for LacI binding, but does not itself bind to the LacI-promoter complex. | + | In the simpler model ({{ref|2}}) IPTG competes with free promoter for LacI binding, but does not itself bind to the LacI-promoter complex. |
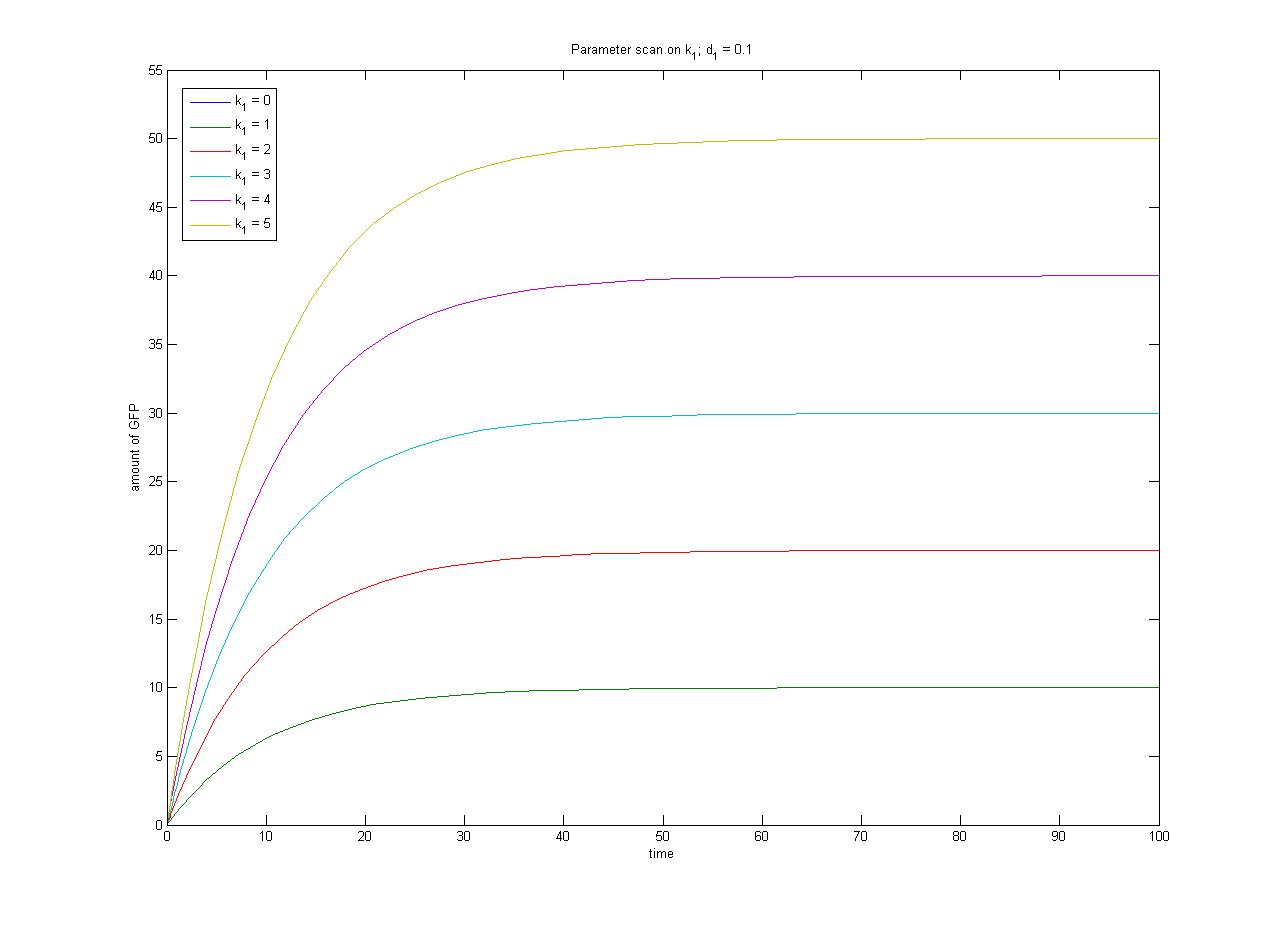
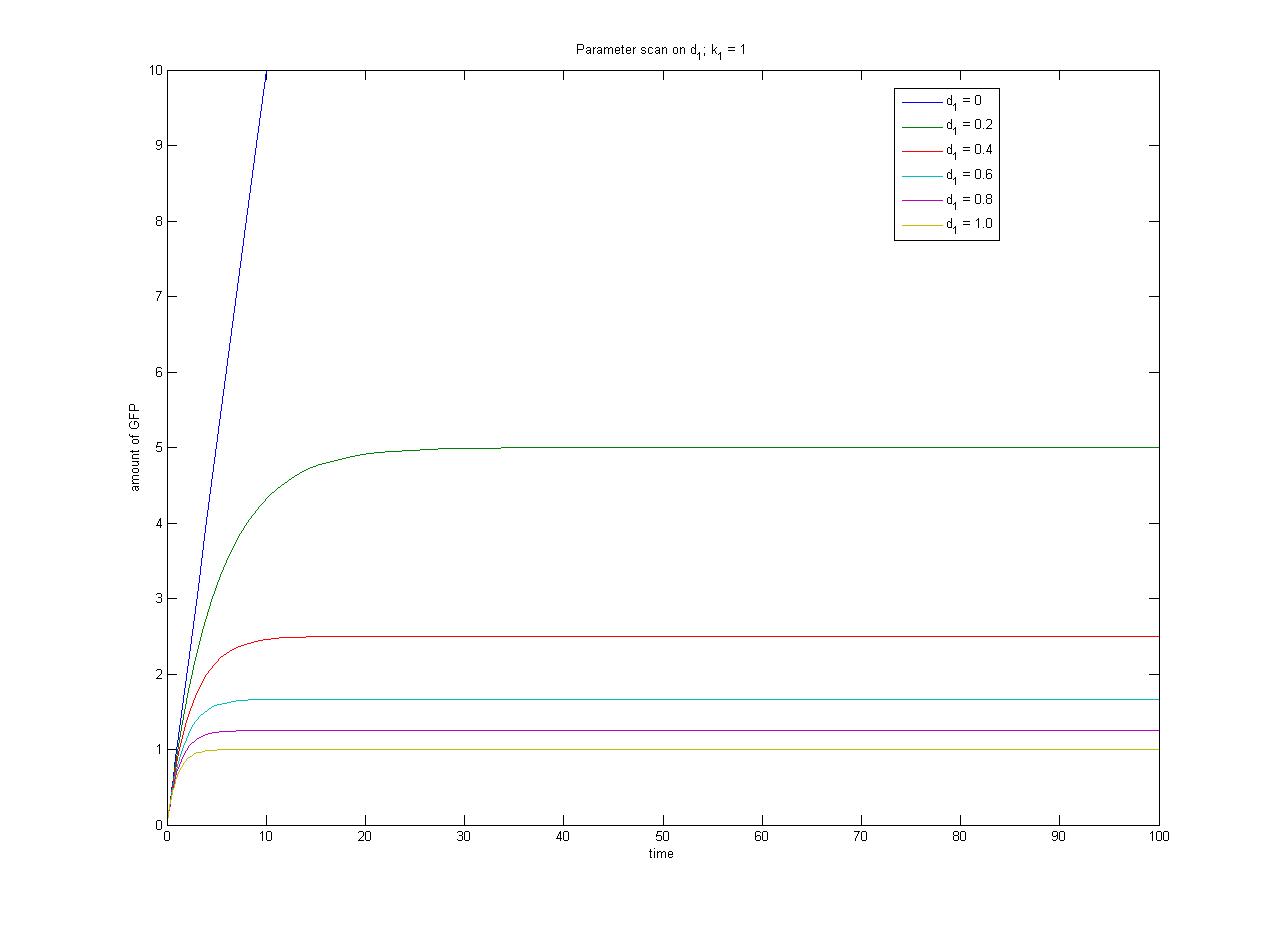
Assuming this model, all else equal, the steady-state concentration of free promoter and hence the steady-state concentration of GFP are independent of the initial concentration of IPTG. | Assuming this model, all else equal, the steady-state concentration of free promoter and hence the steady-state concentration of GFP are independent of the initial concentration of IPTG. | ||
| Line 71: | Line 71: | ||
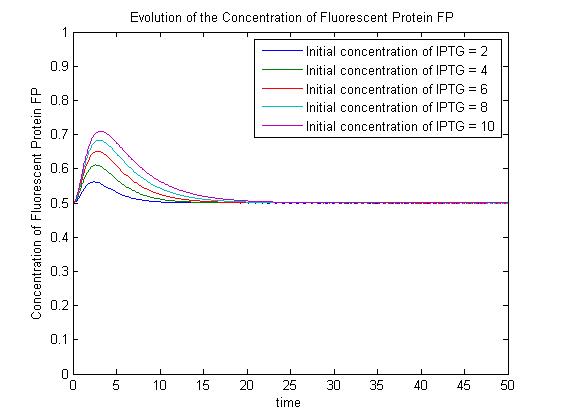
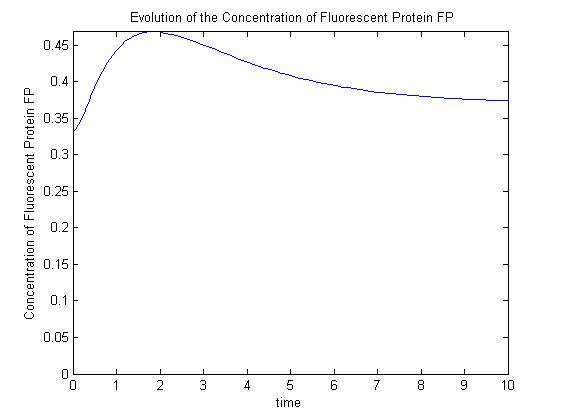
The pre-steady-state dynamic behaviour of the GFP concentration will differ with different initial concentrations of IPTG (but the steady-state behaviour will not). Hence, accuarate data collection during the pre-steady-state phase is crucial for paramater estimation. | The pre-steady-state dynamic behaviour of the GFP concentration will differ with different initial concentrations of IPTG (but the steady-state behaviour will not). Hence, accuarate data collection during the pre-steady-state phase is crucial for paramater estimation. | ||
| - | A more sophisticated model allows for interaction between IPTG and the promoter-LacI complex | + | A more sophisticated model allows for interaction between IPTG and the promoter-LacI complex ({{ref|3}}). Under this model, the dynamic behaviour (whether or not [GFP] attains a maximum higher than its steady-state value) depends on the relative strengths of the kinetic constants describing the interactions underlying the model. Either way, all else equal the steady-state [GFP] will vary as a Hill-function dependent on the initial concentration of IPTG; this characteristic can be used to discriminate between the two models. |
[[Media:InduciblePromoter_ODE.m|ODEs]]<br> | [[Media:InduciblePromoter_ODE.m|ODEs]]<br> | ||
Revision as of 16:17, 21 October 2008
Modelling the Genetic Circuit
|
|||||||||||||||||||||||||
 "
"