Team:BCCS-Bristol/Modeling-GRN
From 2008.igem.org
(→Transport) |
(→Transport) |
||
| Line 57: | Line 57: | ||
<math>$ alpha $</math> | <math>$ alpha $</math> | ||
&alpha | &alpha | ||
| + | |||
| + | <math>\sqrt{1-e^2}</math> | ||
| + | |||
| + | <math>\sqrt{2}</math> | ||
We were interested in understanding the relationship between AHL production at a point and | We were interested in understanding the relationship between AHL production at a point and | ||
Revision as of 14:22, 23 October 2008
Contents |
Gene Regulatory Networks (GRN) Modelling
Introduction
Sender
The sender device consists of two genes (LuxI, GFP) and a single promoter (pCpxR). We are interested in the relationship between the activator protein CpxR and the production of the signalling compound N-acyl-homoserine lactone (AHL). AHL is produced by the LuxI enzyme which uses S-adenosylmethionine and the acylated-acyl carrier protein as substrates for the reaction. The concentration of the activator protein CpxR is specified as a contact profile mimicking the discovery of a particle. A linear piece-wise function was selected, ranging from 0 at t = 0, to a maximal CpxR protein concentration CpMax after 1 hour, taken from [15]. In the following equation time t is measured in minutes,
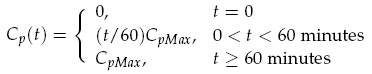
Both LuxI and GFP are controlled by the promoter pCpxR. In reality, because both genes are under the control of a single promoter, transcription would lead to the creation of a single mRNA strand. This mRNA would contain both genes, however, have separate ribosome binding sites (RBS) for each to allow for parallel translation. Due to the negligible effect on dynamics and a lack of information regarding degradation rates of this mRNA sequence, each gene transcription was treated separately. The transcription phase was modelled using a Hill function for the activation of the promoter with a degradation term for existing mRNA. This gives the following for mRNA concentrations of LuxI Im and GFP Gm:
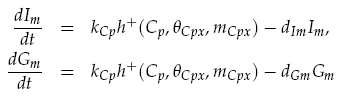
Translation of the mRNAs into proteins of LuxI Ip and GFP Gp was modelled as proportional to the current mRNA concentrations minus a degradation term, yielding the model:

Transport
<math>\alpha\,\!</math> <math>&alpha</math> <math>$ alpha $</math> &alpha
<math>\sqrt{1-e^2}</math>
<math>\sqrt{2}</math>
We were interested in understanding the relationship between AHL production at a point and the spatial concentration distribution over time. For the transportation of AHL between cells we assumed diffusion was the only process taking place. There is some evidence that AHL may be actively transported across cell membranes [8], however, by assuming only diffusion, a good indication of the worse case scenario could be gained. Assuming the diffusion co-efficient D is the same in all directions we have,
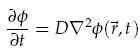
where f(~r, t) is the concentration of the diffusing chemical at location ~r and time t. As evolution of the concentration distribution is the same in all directions, we only considered a 1-dimensional case. The following ‘Forward Time Centred Space’ (FTCS) discrete numerical scheme was used to calculate the time evolution of the system, namely we have:
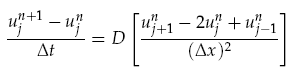
where unj<math>\u^n_j</math> is the chemical concentration at the discrete spatial index j and time index n, Dt is the time step, and Dx is the width of each spatial index. When computing the time evolution, the spatial environment was split into 1mm portions and a time step of 0.01s used.
Reciever
 "
"