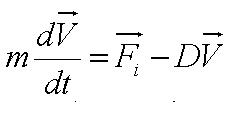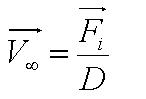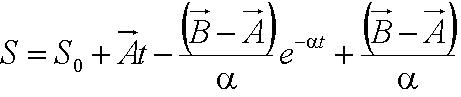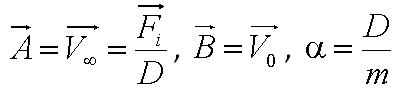Team:Imperial College/Motility
From 2008.igem.org
(Difference between revisions)
| Line 1: | Line 1: | ||
{{Imperial/StartPage2}} | {{Imperial/StartPage2}} | ||
=== Motility Analysis === | === Motility Analysis === | ||
| - | {{Imperial/Box2|| | + | {{Imperial/Box2|Approach| |
<br> | <br> | ||
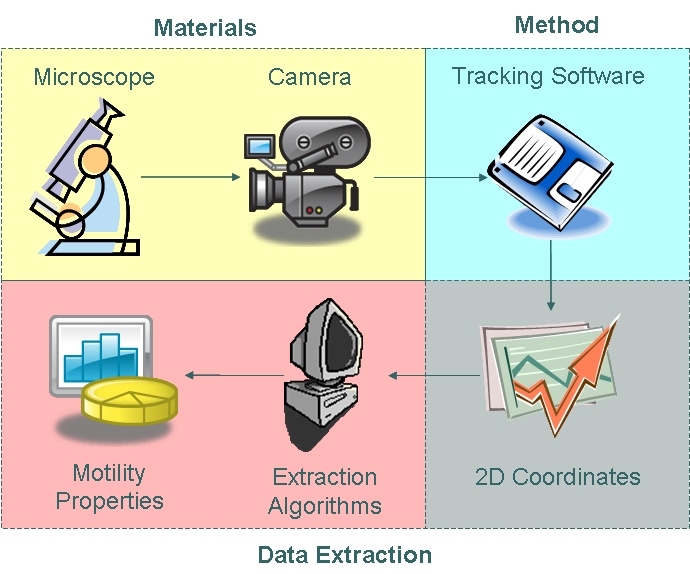
As part of our chasis characterisation process, we have decided to model ''B. subtilis'' motility. In order to do this, the approach illustrated below was taken. The first phase of modelling involved data collection using microscopy techniques and cell tracking. Collected data was then analysed using algorithms which enabled us to extract distributions of parameters as defined in our model. | As part of our chasis characterisation process, we have decided to model ''B. subtilis'' motility. In order to do this, the approach illustrated below was taken. The first phase of modelling involved data collection using microscopy techniques and cell tracking. Collected data was then analysed using algorithms which enabled us to extract distributions of parameters as defined in our model. | ||
| Line 20: | Line 20: | ||
{{Imperial/Box1|Motility Model| | {{Imperial/Box1|Motility Model| | ||
| + | <br> | ||
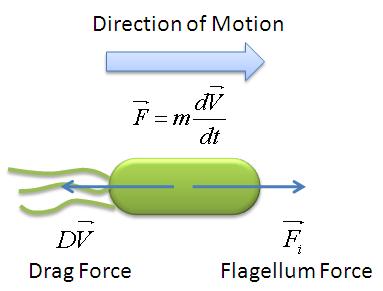
The following mechanical model was developed. | The following mechanical model was developed. | ||
| Line 28: | Line 29: | ||
Solving this first order ODE, we derive an expression for cell velocity: | Solving this first order ODE, we derive an expression for cell velocity: | ||
| - | [[Image:Velocity.JPG|200px | + | <center>[[Image:Velocity.JPG|200px]], where [[Image:Para_1.JPG|90px]]</center><br> |
| - | where [[Image:Para_1.JPG|90px]]<br> | + | |
Solving the first order ODE for displacement, we derive an expression for cell trajectory: | Solving the first order ODE for displacement, we derive an expression for cell trajectory: | ||
| Line 36: | Line 36: | ||
[[Image:Parameter.JPG|250px|center]]<br> | [[Image:Parameter.JPG|250px|center]]<br> | ||
| - | In this model, we attempt to obtain a distribution for the flagellar force, which is represented by parameter ''A''. We assume that the medium is homogenous and the drag coefficient is constant throughout the medium, hence the distribution of flagellar force will be sufficiently be described by parameter A. | + | In this model, we attempt to obtain a distribution for the flagellar force, which is represented by parameter ''A''. We assume that the medium is homogenous and the drag coefficient is constant throughout the medium, hence the distribution of flagellar force will be sufficiently be described by parameter A.|}} |
| - | + | {{Imperial/Box2|Results| | |
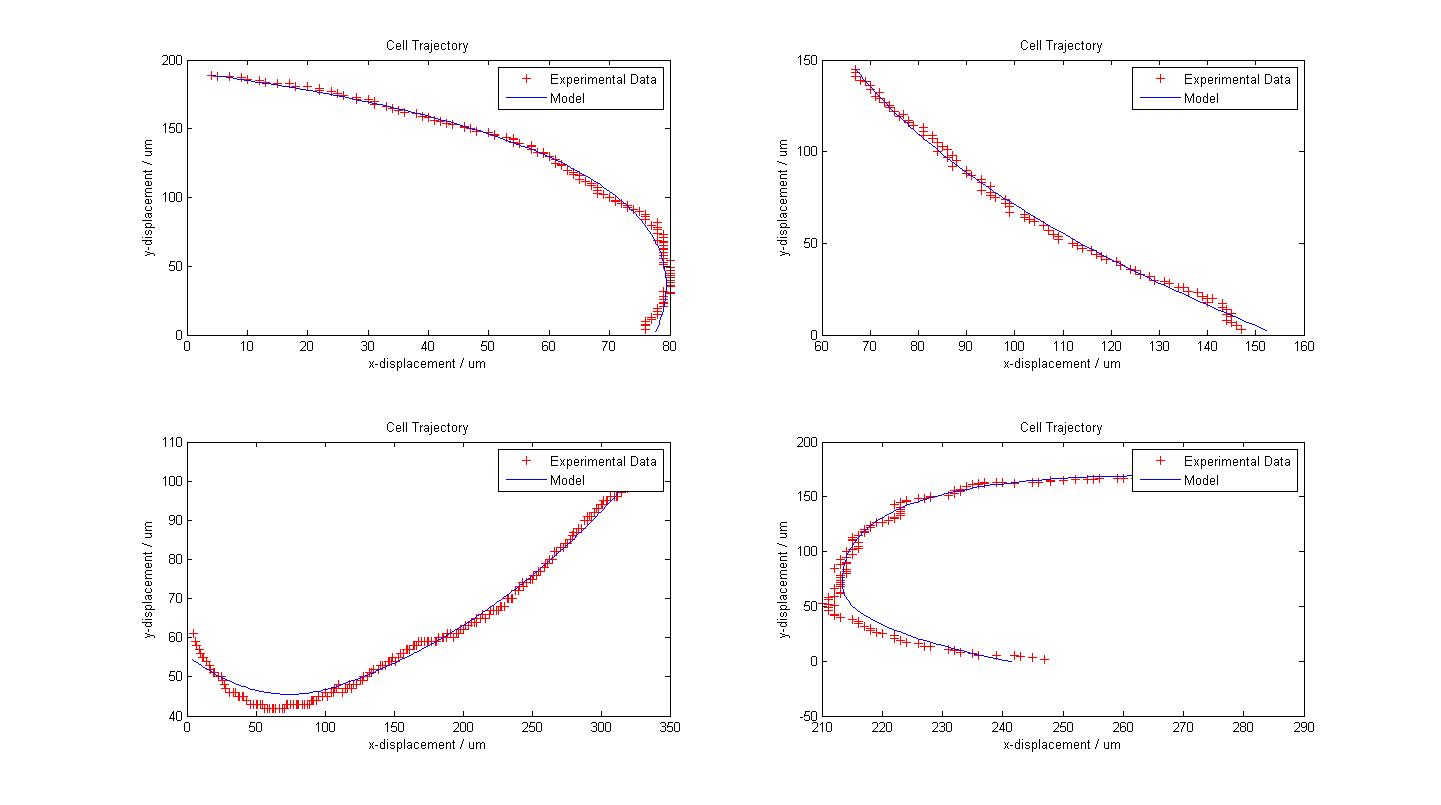
The following figure shows the results of our model fitting. We have introduced a change in flagellar force at certain points of the cell trajectory so as to achieve a better fit. A maximum of two runs were allowed for each cell trajectory. | The following figure shows the results of our model fitting. We have introduced a change in flagellar force at certain points of the cell trajectory so as to achieve a better fit. A maximum of two runs were allowed for each cell trajectory. | ||
| Line 44: | Line 44: | ||
[[Image:Fitted_Models.jpg|450px|center]]<br> | [[Image:Fitted_Models.jpg|450px|center]]<br> | ||
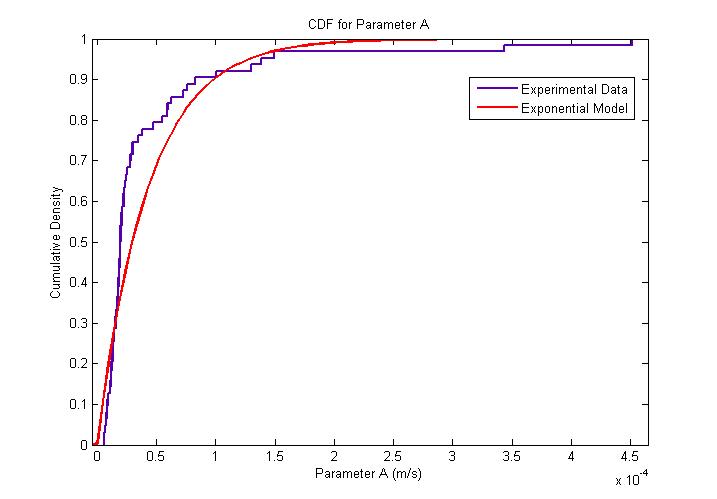
| - | The distribution of parameter A was | + | The MATLAB Distribution Fitting Tool was used to model the distribution of parameter A. Parameter A was found to be exponentially distributed. The following figures describe the probability density function and cumulative density function. |
| - | [[Image: | + | [[Image:Exponential_Distribution_for_Parameter_A_PDF.jpg|450px|center]]<br> |
| - | [[Image: | + | [[Image:Exponential_Distribution_for_Parameter_A_CDF.jpg|450px|center]]<br> |
| + | |}} | ||
{{Imperial/EndPage|Genetic Circuit|Appendices}} | {{Imperial/EndPage|Genetic Circuit|Appendices}} | ||
 "
"