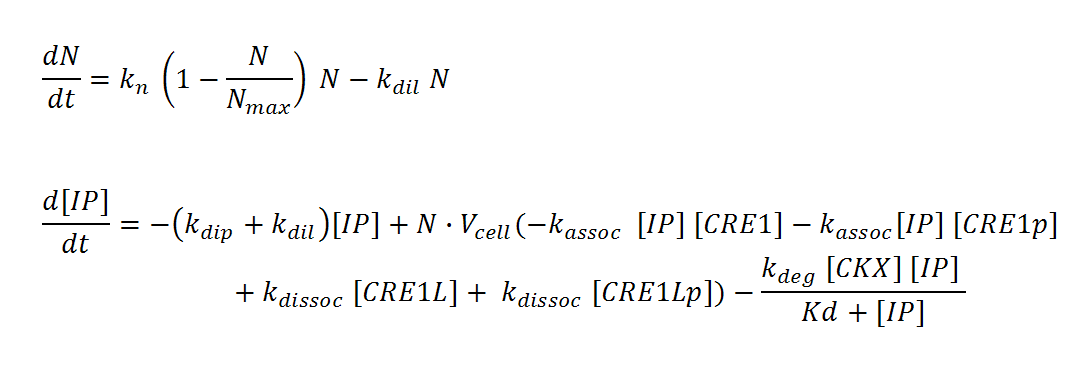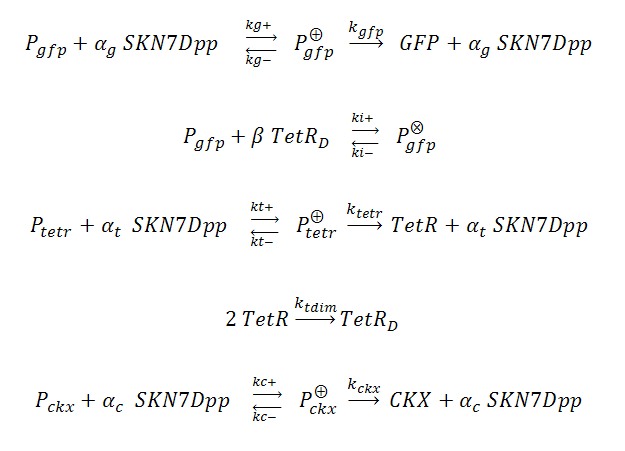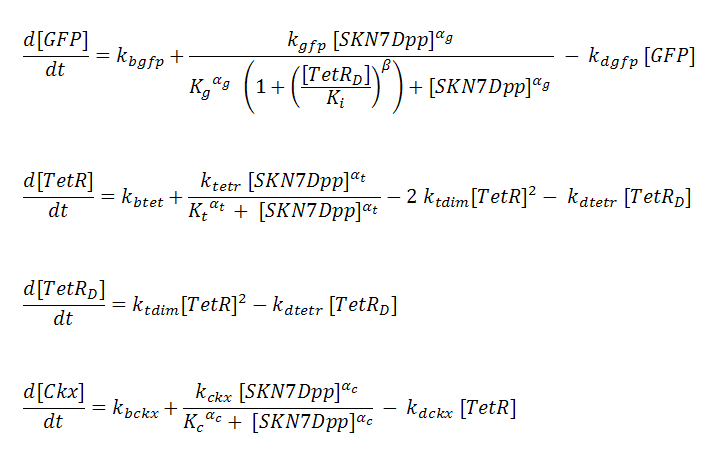Team:University of Ottawa/Modeling

From 2008.igem.org

(Difference between revisions)
(→Pulse Characteristics)
(→Pulse Characteristics)
Line 170: Line 170:
***Catalytic constant and Michaelis constant for the CKX enzyme – these values were obtained from the literature
***Catalytic constant and Michaelis constant for the CKX enzyme – these values were obtained from the literature
***modified by: the addition of a suitable electron acceptor to the media [ ].
***modified by: the addition of a suitable electron acceptor to the media [ ].
 +
 +
First, we wanted to characterize the nature of the “pulses” produced under a constant input signal of IP (10 uM). The pulses are relatively long (usually 6-10hrs), but it must be noted that contrary to this particular case, in the application of recombinant protein expression one would normally have the protein tagged for secretion. Continuous export would accelerate the down phase of the GFP pulse.
 +
 +
The overall shape of the GFP pulse appeared to be very sensitive to the interplay between the kinetics of SKN7-mediated GFP transcription and TetR-mediated GFP repression. The faster TetR accumulates, the faster GFP expression is attenuated, and thus the shorter the pulse. However, there appears to be a trade-off in that faster TetR expression will also diminish the maximum expression level that GFP can attain, thus shorter pulses tend to have smaller amplitudes.
 +
To illustrate this effect, we show a simplified case where the binding and repression of GFP expression by the TetR dimer is subject to a threshold concentration of TetR. That is, TetR will only bind to the GFP promoter once it reaches a threshold concentration. This allows a gateway of time for GFP levels to rise to significant levels before being attenuated by TetR.
 +
 +
When the threshold concentration is set to 0.001uM, the result is an idealized pulse shape, biexponential-like with a sharp spike. However, if the Tet threshold is set too high, TetR is unable to completely repress GFP expression and instead GFP reaches a new, higher steady state level (although lower than it would be in the absence of TetR). Notice that the threshold level has a significant effect on the amplitude of the pulse.

Revision as of 16:57, 27 October 2008


Untitled Document

 

 


counter create hit

Modeling

Variables Our models contain the following variables and species:

Species table.jpg

Reactions

Parameters The values for the parameters governing expression of the core signaling components (IP, CRE1, YPD1, SKN7) were taken from the model of Chen and Weiss []. The parameters specific to our system were either gleaned from other sources if available, or were varied within reasonable ranges to explore their effect on the dynamics of the system.

Receiver cells

N, M and IP are total culture variables. Cell density (N, M) is modeled as logistic growth, with carrying capacity Nmax, Mmax. Continuous culture dilution may be chosen rather than batch culture by setting a nonzero dilution rate (kdil). Inducer concentration (IP) in the reactor is affected by an overall degradation rate (kdip), the culture dilution rate (kdil), and binding/releasing of the molecule to the receptor in both its phosphorylated (CRE1p) and non-phosphorylated (CRE1) state. IP is assumed to diffuse rapidly across the cell membrane so that intracellular and total culture IP concentrations are the same at all times. The effective “receptor concentration” in the total reactor volume (mol receptors/culture volume) is estimated by multiplying the cellular concentration of receptors (mol receptors per cell/cell volume) by the cell density times cell volume. Simple Michaelis-Menten kinetics is used to model enzyme-mediated degradation of IP by CKX. With these assumptions, we derive the differential equations below.

N IP.png

It is assumed that IP binds CRE1 with 1:1 stoichiometry. Ligand-bound CRE1 autophosphorylates and transfers its phosphate to the second messenger YPD1. The response protein SKN7 forms a dimer SKN7D. SKN7D is phosphorylated twice via reversible phosphor-transfer by YPD1. The double phosphorylated SKN7Dpp is the active transcription factor. The differential equations are adapted from Chen and Weiss []; the kinetics for the reactions are approximated using elementary mass action kinetics. These equations represent the changes in a single cell of the population. More precisely, they represent the single cell dynamics averaged over the whole population.

SKN7.png

In our system, three genes are under the control of SKN7Dpp: the gene of interest (GFP) is expressed fastest, followed by expression of the TetR repressor, which dimerizes and binds to tet operator (tetO) elements upstream of the GFP cassette, inhibiting its expression and thus creating a “pulse” of GFP. Meanwhile, the product of the third SKN7-induced gene, cytokinin dehydrogenase (CKX), accumulates and degrades IP in the culture, allowing the system to reset itself for another pulse. The GFP, TetR and CKX genes are regulated by different promoters each possessing synthetic SKN7 response elements (SSRE).

React.png

P_^⨁ represents the activator-bound promoter, while P_^⨂ represents repressor-bound promoter. TetR binding is assumed to block access of SKN7Dpp to the promoter. Transcription is considered to be rate limiting for gene expression and the kinetics for transcription are modeled as Hill-type. Using the pre-equilibrium assumption for binding of the transcriptional activator SKN7Dpp and repressor TetR to their respective sites on the promoters, we can derive the following equations from the reactions above:

GFPeqs.jpg

To test the behavior of our pulse generator, simulations were run using MatLab. For example, the diagram below shows the change in concentration of each of the species during a simulation of the pulse generator (receiver) strain responding to an initial spike in inducer (IP) concentration:

Here it is assumed that cells are growing in a continuous culture bioreactor (or, equivalently, a batch reactor in which a fraction of the culture is periodically replaced with fresh media). The dilution rate is set to maintain the cell density at around 1 million/mL. The initial concentration of IP is set at 10uM.

Receiversim.jpg

Pulse Characteristics

For the functioning of the core pulse generator motif, important parameters include:

  • SKN7 transcription kinetics
    • kgfp, ktet, kckx
      • max transcriptional output for each of the three genes
      • modified by: TATA box mutations
    • Kg, Kt, Kc
      • The Hill constants for binding of the SKN7Dpp transcription factor to the SSRE elements (actual dissociation constant for the interaction between SSRE and SKN7Dpp was not known, this value was varied from the uM to nM range in our simulations)
      • odified by: using either the single or tandem SSRE configuration in our pSSRE promoters
    • αg,, αt, αc
      • The Hill coefficients for binding of SKN7Dpp transcription factor to the SSRE elements
  • TetR repression kinetics
    • Ki
      • Hill constant for binding of TetRD to the tet operator of the GFP cassette
      • Modified by: using single or multiple tet operator elements
    • β
      • Hill coefficient for binding of TetRD to the tet operator of the GFP cassette
  • CKX enzyme kinetics
    • Kdeg, Km
      • Catalytic constant and Michaelis constant for the CKX enzyme – these values were obtained from the literature
      • modified by: the addition of a suitable electron acceptor to the media [ ].

First, we wanted to characterize the nature of the “pulses” produced under a constant input signal of IP (10 uM). The pulses are relatively long (usually 6-10hrs), but it must be noted that contrary to this particular case, in the application of recombinant protein expression one would normally have the protein tagged for secretion. Continuous export would accelerate the down phase of the GFP pulse.

The overall shape of the GFP pulse appeared to be very sensitive to the interplay between the kinetics of SKN7-mediated GFP transcription and TetR-mediated GFP repression. The faster TetR accumulates, the faster GFP expression is attenuated, and thus the shorter the pulse. However, there appears to be a trade-off in that faster TetR expression will also diminish the maximum expression level that GFP can attain, thus shorter pulses tend to have smaller amplitudes. To illustrate this effect, we show a simplified case where the binding and repression of GFP expression by the TetR dimer is subject to a threshold concentration of TetR. That is, TetR will only bind to the GFP promoter once it reaches a threshold concentration. This allows a gateway of time for GFP levels to rise to significant levels before being attenuated by TetR.

When the threshold concentration is set to 0.001uM, the result is an idealized pulse shape, biexponential-like with a sharp spike. However, if the Tet threshold is set too high, TetR is unable to completely repress GFP expression and instead GFP reaches a new, higher steady state level (although lower than it would be in the absence of TetR). Notice that the threshold level has a significant effect on the amplitude of the pulse.

Retrieved from "http://2008.igem.org/Team:University_of_Ottawa/Modeling"