User:Federico Castro M/Horizontal Transfer/Models Simulations
From 2008.igem.org
(mathematical modeling editing) |
(image added) |
||
| Line 14: | Line 14: | ||
in turn by a change of sign in the growth rate. For those in which horizontal transport has not taken place yet it becomes negative, while for the third kind, already resistant to both ampicillin and tetracycline a new logistic equation with positive growth rate is used. | in turn by a change of sign in the growth rate. For those in which horizontal transport has not taken place yet it becomes negative, while for the third kind, already resistant to both ampicillin and tetracycline a new logistic equation with positive growth rate is used. | ||
| - | This is seen in the figures. In the first one both curves increase, while in the second two decrease (corresponding to | + | This is seen in the following figures. In the first one both curves increase, while in the second two decrease (corresponding to |
the nonresistent types) and a third increasing curve corresponding to the strain resistent to both. | the nonresistent types) and a third increasing curve corresponding to the strain resistent to both. | ||
| + | {| | ||
| + | |[[Image:Fig3UNAMIPN.JPG |460px]] | ||
| + | |[[Image:Fig4UNAMIPN.JPG |400px]] | ||
| + | |} | ||
Revision as of 18:00, 29 October 2008
The mathematical study and simulations are based on population dynamics models. We assume that each bacterium type grows according to a logistic equation:
where a is the growth rate and K is the carrying capacity. Therefore, type A and B have a specific grow rate and carrying capacity, since they are in a medium where only one antibiotic is present, to which each one is resistent.
Later on, both populations are exposed to the two antibiotics in lethal concentrations and so only those bacteria that have acquired resistence to the other antibiotic will be able to survive. This is represented in turn by a change of sign in the growth rate. For those in which horizontal transport has not taken place yet it becomes negative, while for the third kind, already resistant to both ampicillin and tetracycline a new logistic equation with positive growth rate is used.
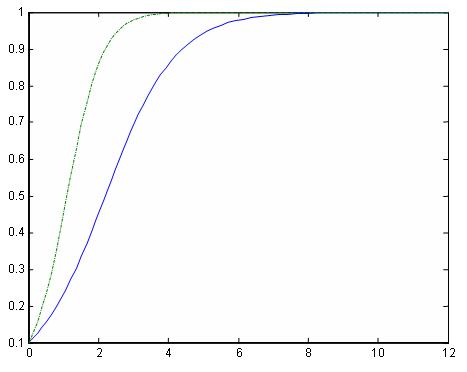
This is seen in the following figures. In the first one both curves increase, while in the second two decrease (corresponding to the nonresistent types) and a third increasing curve corresponding to the strain resistent to both.
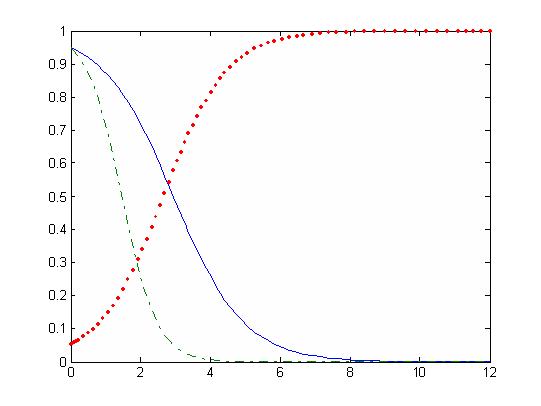
| 
|
 "
"
