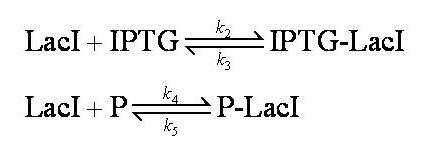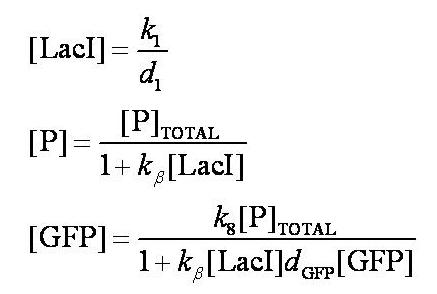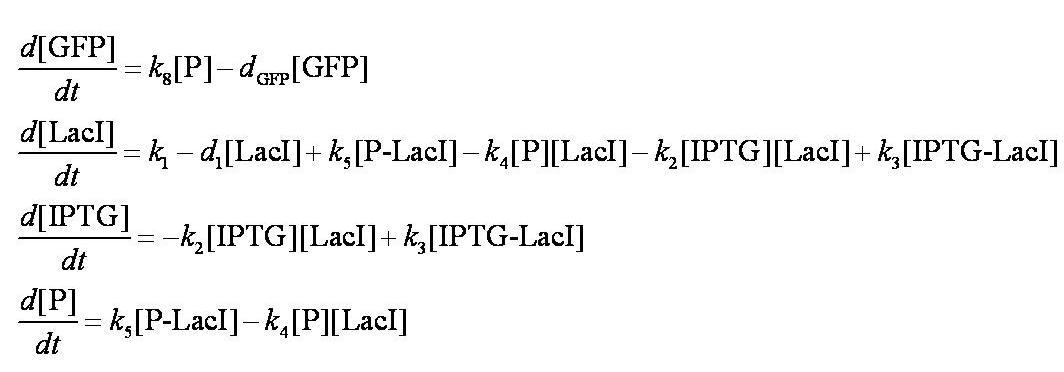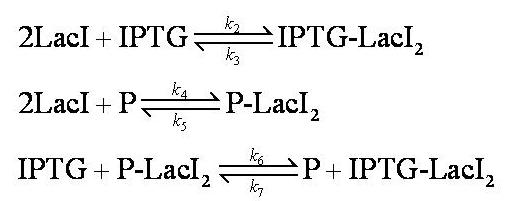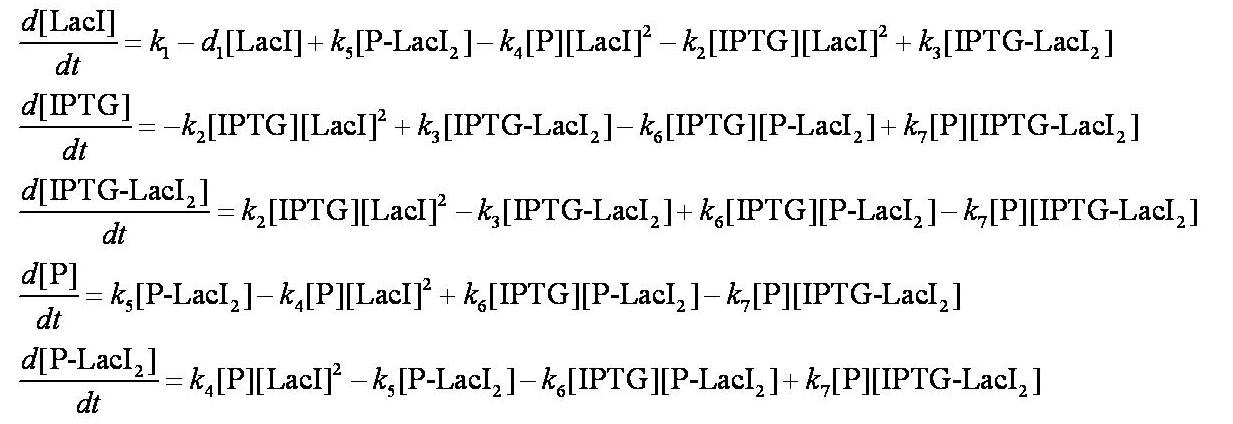Team:Imperial College/Genetic Circuit Details
From 2008.igem.org
m |
|||
| Line 32: | Line 32: | ||
}} | }} | ||
| - | {{Imperial/Box1|More Sophisticated Model({{ref|2}})| | + | {{Imperial/Box1|More Sophisticated Model ({{ref|2}})| |
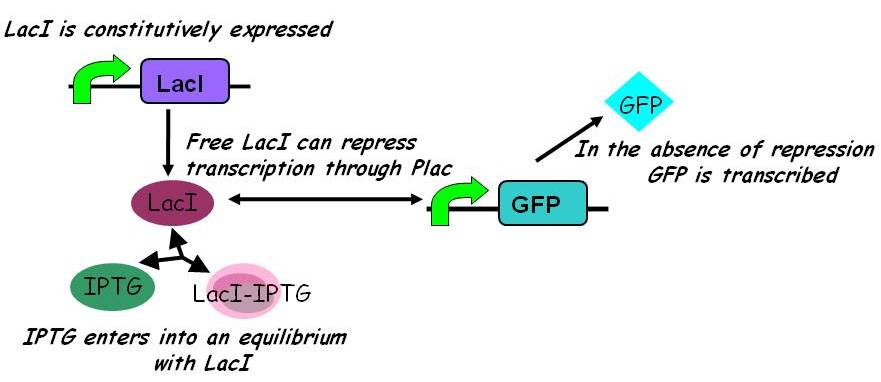
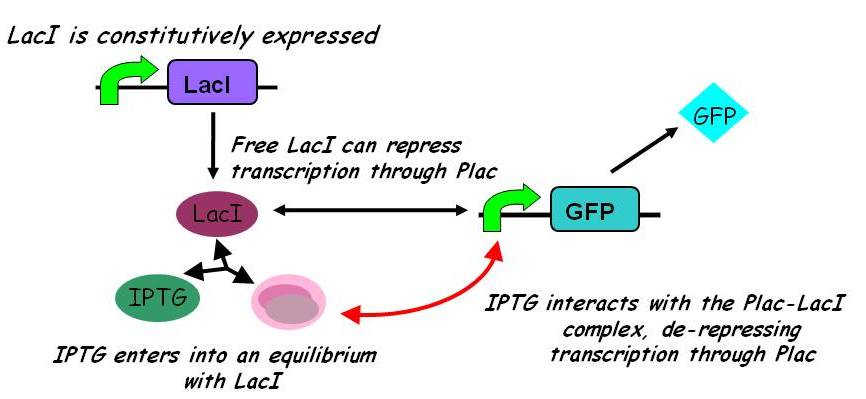
[[Image:Inducible_promoters_2.jpg|450px]] | [[Image:Inducible_promoters_2.jpg|450px]] | ||
| - | ====Equilibria==== | + | ====== Equilibria ====== |
[[Image:Complex_model_equilibria.jpg|350px]] | [[Image:Complex_model_equilibria.jpg|350px]] | ||
| Line 46: | Line 46: | ||
Note: k<sub>2</sub>, k<sub>3</sub>, k<sub>4</sub>, k<sub>5</sub>, k<sub>6</sub> and k<sub>7</sub> represent binding constants for formation and dissociation of complexes. | Note: k<sub>2</sub>, k<sub>3</sub>, k<sub>4</sub>, k<sub>5</sub>, k<sub>6</sub> and k<sub>7</sub> represent binding constants for formation and dissociation of complexes. | ||
| - | ====Equations==== | + | ====== Equations ====== |
Before IPTG is introduced the system is in a steady state: | Before IPTG is introduced the system is in a steady state: | ||
| Line 64: | Line 64: | ||
These are evaluated numerically using Matlab's ODE solver. | These are evaluated numerically using Matlab's ODE solver. | ||
| - | ====Qualitative effect of parameters on behaviour==== | + | ====== Qualitative effect of parameters on behaviour ====== |
Two different regimes of behaviour can be exhibited by the concentration of GFP over time as described by the more complex model, dependent on the parameters defining the ODE system. | Two different regimes of behaviour can be exhibited by the concentration of GFP over time as described by the more complex model, dependent on the parameters defining the ODE system. | ||
Revision as of 02:49, 30 October 2008
|
|||||||||||||||
 "
"