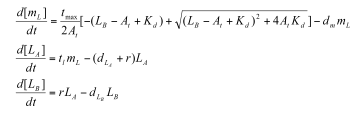Team:Michigan/Project/Modeling/Model1.html
From 2008.igem.org
| Line 15: | Line 15: | ||
*tl=translation rate | *tl=translation rate | ||
*r = conversion rate from La to Lb | *r = conversion rate from La to Lb | ||
| + | *Kd= dissociation constant of NifL and Nifa (= kr/kf, where kf is the forward binding rate of NifL and NifA and kr is the rate of decomposition of the NifL/NifA complex) | ||
*any d= degradation rate of that species | *any d= degradation rate of that species | ||
| - | + | Professor Daniel Forger came up with this model for the Sequestillator. This simple system assumes the total amount of NifA in the system is constant, and considers three variable: NifL mRNA (mL), NifL (La), and a simple covalent modification of NifL (Lb). The quadratic mRNA production function comes from making rapid equilibrium assumptions (see box to the right of the equations. A= free unbound NifA, L = unbound NifL). From analyzing this small model, we were able to see that in order for oscillations to exist, there needed to be a tight binding between NifL and NifA (i.e., Kd is very small) and one-to-one titration of NifL and NifA (the mRNA production function = tmax*A/At, where A is free NifA in the system. A graph of the function vs. Lb is a oblique line). | |
| - | This simple system assumes the total amount of NifA in the system is constant, and considers three variable: NifL mRNA (mL), NifL (La), and a simple covalent modification of NifL (Lb). | + | We used the Indexilator to make some "relative" Ninfa index searches. |
<div align='center'>[[Image:chart.png]]<br> | <div align='center'>[[Image:chart.png]]<br> | ||
Revision as of 00:47, 30 October 2008
|
|---|
|
Sequestillator Model 1: A simple modelParameters:
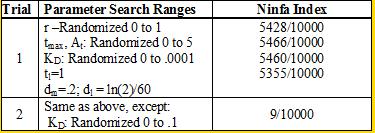
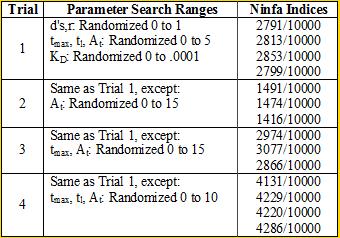
Professor Daniel Forger came up with this model for the Sequestillator. This simple system assumes the total amount of NifA in the system is constant, and considers three variable: NifL mRNA (mL), NifL (La), and a simple covalent modification of NifL (Lb). The quadratic mRNA production function comes from making rapid equilibrium assumptions (see box to the right of the equations. A= free unbound NifA, L = unbound NifL). From analyzing this small model, we were able to see that in order for oscillations to exist, there needed to be a tight binding between NifL and NifA (i.e., Kd is very small) and one-to-one titration of NifL and NifA (the mRNA production function = tmax*A/At, where A is free NifA in the system. A graph of the function vs. Lb is a oblique line). We used the Indexilator to make some "relative" Ninfa index searches. We see that if we increase our search range for the dissociation constant to 0 to .1, then we get a substantially less Ninfa index, illustrating the importance of having a tight binding between NifA and NifL. We again see the necessity of a tight binding between NifA and NifL |
|---|
 "
"