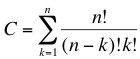Team:ETH Zurich/Project/Approach

Our Approach

The concept we are trying to follow is based on a massively parallel random search. We have developed a top-down approach that will enable us to dramatically reduce the genome size of a living organism. As we described in the previous section we are looking for a minimal subset of genes that are able to sustain life. The main problem when following this type of approach is the combinatorial possibilities that lead to a hugh solution space, this corresponds to a classical NP-problem (non-polynomial) in computer science. The number of combinations of the original set of genes is given by:

This type of problem makes it infeasible to try all possible combinations sequentially and justifies a massively parallel approach as the one followed in this project.

To achieve this, we start with our wild type genome and generate a large library of mutants by randomly deleting fragments of the chromosome as described in the genome reduction section.

We are following an approach based on random genome deletions and a designed selection mechanism to reach our goal. As mentioned in the motivation section, we postulate that a random disruption of genes combined with an evolutionary approach will allow us to dramatically reduce the genome size of an organism.

In order to prove the viability of the concept, we have developed a series of models and of biological experiments that are introduced in this section. For details on the results of the single steps we refer to the specific sections in the Wetlab and the Modelingsections. Figure 1 gives an overview of the developed system and illustrates the final experimental setup.

We start by inoculating our continuous culture with a wild type strain with a knock out that makes it auxotroph for nucleotides. These nucleotides will be the limiting substrate in the chemostat and the concentration in our feed will be the parameter we can tune to set the selective pressure. See the chemostat selection section for a detailed description of the selection process.

The iteration of the following steps gradually reduces the size of the chromosome:

1) Excision of genomic sequences by restriction enzymes and ligases. We have developed a genetic circuit that allows us to generate a controlled pulse to control the expression of restriction enzymes and ligases. Our assumption is that by carefully selecting the timing of the pulse, we can cut fragments of the chromosome, that in a number of cases will be lost when the chromosome is religated. To test this principle in vivo we have developed a proof of concept that will show the potential viability of this method (genome reduction). 2)

See the chemostat model section for a detailed description of the selection process.

a) .. excision of genomic sequences by restriction enzymes can be performed within the living cell; b) .. fragmented genomic DNA can be ligated inside the living cell by simultaneous expression of T4 ligase; c) .. pulse generators that produce pulses of protein expression of variable length terminated by induction with a second compound can be devised both on the transcriptional as well as on the translational level; d) .. cells with optimized growth and reproduction can be selected by competition inside chemostat cultures.

Random walk towards a minimal genome