Team:BCCS-Bristol/Modeling

From 2008.igem.org

(Difference between revisions)
(→Tools)
(→Modelling Parameters)
Line 97: Line 97:
=== Modelling Parameters ===
=== Modelling Parameters ===
 +
 +
 +
{| {{table}}
 +
| align="center" style="background:#f0f0f0;"|'''Attribute'''
 +
| align="center" style="background:#f0f0f0;"|'''Value'''
 +
| align="center" style="background:#f0f0f0;"|'''Strain'''
 +
| align="center" style="background:#f0f0f0;"|'''Justification'''
 +
|-
 +
| Length||2μm||MG1655||Values come from the University of Alberta’s datasheet on MG1655, produced to aid modelling. Variability in size between strains - for instance, AW405 length varies between 1.5±0.2μm. But University of Alberta datasheet is specifically for MG1655.
 +
|-
 +
| Diameter||0.8μm||MG1655||
 +
|-
 +
| Shape||Circle r =0.714μm||||Actually rod-like. A circle with r= 0.714μm will have equivalent surface area to rod-like.
 +
|-
 +
| Mass||1.02x10-13g||MG1655||Given 1x10-12g for cell wet weight. Dividing this by gravity (=9.81) gives mass.
 +
|-
 +
| Swimming Speed||50μms-1||MG1655||University Alberta's datasheet gives 50μms-1. However, Swimming speed is affected by: 
 +
 +
• Viscosity (as viscosity increases the speed increases to some maximum, then decreases as the viscosity increases further. E.coli (strain:KL227 of length: 1.0μm and diameter: 0.5μm) maximum speed occurs at viscosity 8cp. Suggested to be because higher viscosity provides increased energy supply. 
 +
 +
• Temperature
 +
 +
• Culture medium
 +
 +
• Vary strain to strain.
 +
 +
• Experimental methods Many papers give different and variable speeds (mainly for AW405 ~20μms-1). The speed itself is nearly uniform during the run. May need to measure experimentally, don't know under what conditions University of Alberta. Alberta value is higher than other values, but probably because MG1655 is a motile strain.
 +
|-
 +
| Tumbling angle||Shape parameter 4 Scale parameter 18.32 Location parameter -4.6||AW405||Appears not to be dependant on the concentration gradient of chemoattractants/repellents. Nor is there correlation between the length of the run and the change in direction. Used a gamma distribution that fitted the data of Berg and Brown. Non normality observed by several groups. Suggestions that non-normality was only due to the experimental methods used e.g. in the capillary tube. Tumbling occurs when 1 or several of the flagella are released from the bundle. The flagella on transition from the bundle to release go from normal (a left-handed helix with a pitch of 2.3  m and a diameter of 0.4  m) to semi coiled (a right-handed helix with half the normal pitch but normal amplitude) and then curly (a right-handed helix with half the normal pitch and half the normal amplitude). This therefore suggests that the tumbling angle has bidirectionality.
 +
|-
 +
| Tumble angle||Bidirectional||AW405||Personal communication with Howard Berg. "The direction is random, more or less, but there is a slight forward bias. It varies from tumble to tumble.  The turn-angle distribution peaks at 68 deg rather than 90 deg.
 +
Tumbles turn out to be more complex than believed in 1972.  Motors switch independently, and a tumble can occur if one or just a few motors change their directions of rotation.  Tumbles are short, as judged by the tracking microscope, because they involve filament physics rather than motor physics:  a transformation in polymorphic form, following motor reversal, from normal to semi-coiled." 
 +
|-
 +
| Tumbling time||0.14±0.19s||AW405||Exponential distribution fitted (stated to be exponential by Berg and Brown) using only the mean tumble length (not STDEV).
 +
|-
 +
| Relationship between tumbling angle and time||||||
 +
|-
 +
| Speed while Tumbling||0μm/s||AW405||Berg and Brown noted that AW405 slowed/stopped while tumbling.
 +
|-
 +
| Isotropic run lengths||0.86±1.18s||AW405||Exponential distribution fitted, this is only an approximate and does not fit exactly (see fig.4 Berg and Brown) The standard deviation is the standard deviation of the mean and has not been used in the exponential distribution
 +
|-
 +
| Drift during run||||AW405||Drift was observed. It is what would be expected from rotational diffusion. (at 2.7cp at 32ºC drift was 23±23°). Rotational Brownian motion cause the cell to veer off course, so that in between tumbles the probability density function f of the swimming direction e evolves according to the Fokker-Planck equation.  Drift velocity in steep gradient of attractant ~7 µm/s (Berg & Turner, 1990)
 +
|-
 +
|
 +
|}

Revision as of 15:39, 1 August 2008

Home The Team The Project Submitted Parts Modelling Wet Lab Calendar Miscellaneous


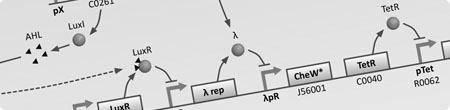
BCCS-Modelling-Header 01.jpg BCCS-Modelling-Header 02.jpg BCCS-Modelling-Header 03.jpg

Contents

Approach

Progress

16/07/08

Random Brownian motion was achieved last Wednesday. Following this we implemented run and tumble motion, this was working by Friday.


23/07/08

Collisions were working (between bacteria and particles). This was modelled with a piece-wise linear potential function.


24/07/08

The gamma distribution (for the sampling of the tumble angle) was improved (on Mario’s recommendation). A tracer for the particles was added.


25/07/08

We went through our assumptions and tweaked the trace to have a colour gradient along its length.

We plan to start implementing chemical signalling gradients.



This is paragraph 2

This is paragraph 3 Italic text Bold text [http://www.google.co.uk Google]

Team Page

This is my This is my text This is my text lhfa lkfahfkljadlkjhfalhdf jkaljf lkh ljkh ljk klah flkjlkj hljkadshf kljhafljkha lkjfh alkj lajkh fljas lfkjh lkjfds lkjhf ljakdhf lkajh flkjhas lkjfha slkjf lakjshf lkjas dlfasldfalskflafldjkah flkjdh dljkfh aldjsh dlskjhf dlkjha ljkfh lajksdhf lksajhdf ldkjashf dlkjsahf lkjdhldfkh adljhas ljkdhfl ajkdhflj This is my textThis is my te
lkdjflsdkjf This is my text lhfa lkfahfkljadlkjhfalhdf jkaljf lkh ljkh ljk klah flkjlkj hljkadshf kljhafljkha lkjfh alkj lajkh fljas lfkjh lkjfds lkjhf ljakdhf lkajh flkjhas lkjfha slkjf lakjshf lkjas dlfasldfalskflafldjkah flkjdh dljkfh aldjsh dlskjhf dlkjha ljkfh lajksdhf lksajhdf ldkjashf dlkjsahf lkjdhldfkh adljhas ljkdhfl ajkdhflj dlskfjdslkjf


h3 h2 h1
32423sa
2344d
2344sd
343sa
234234dsa
324df
432dsgfd
2424ghf
24h
4242dgdff
432gfd
2324dfg
4234fdg

Modelling Parameters

Attribute Value Strain Justification
Length2μmMG1655Values come from the University of Alberta’s datasheet on MG1655, produced to aid modelling. Variability in size between strains - for instance, AW405 length varies between 1.5±0.2μm. But University of Alberta datasheet is specifically for MG1655.
Diameter0.8μmMG1655
ShapeCircle r =0.714μmActually rod-like. A circle with r= 0.714μm will have equivalent surface area to rod-like.
Mass1.02x10-13gMG1655Given 1x10-12g for cell wet weight. Dividing this by gravity (=9.81) gives mass.
Swimming Speed50μms-1MG1655University Alberta's datasheet gives 50μms-1. However, Swimming speed is affected by:

• Viscosity (as viscosity increases the speed increases to some maximum, then decreases as the viscosity increases further. E.coli (strain:KL227 of length: 1.0μm and diameter: 0.5μm) maximum speed occurs at viscosity 8cp. Suggested to be because higher viscosity provides increased energy supply.

• Temperature

• Culture medium

• Vary strain to strain.

• Experimental methods Many papers give different and variable speeds (mainly for AW405 ~20μms-1). The speed itself is nearly uniform during the run. May need to measure experimentally, don't know under what conditions University of Alberta. Alberta value is higher than other values, but probably because MG1655 is a motile strain.

Tumbling angleShape parameter 4 Scale parameter 18.32 Location parameter -4.6AW405Appears not to be dependant on the concentration gradient of chemoattractants/repellents. Nor is there correlation between the length of the run and the change in direction. Used a gamma distribution that fitted the data of Berg and Brown. Non normality observed by several groups. Suggestions that non-normality was only due to the experimental methods used e.g. in the capillary tube. Tumbling occurs when 1 or several of the flagella are released from the bundle. The flagella on transition from the bundle to release go from normal (a left-handed helix with a pitch of 2.3 m and a diameter of 0.4 m) to semi coiled (a right-handed helix with half the normal pitch but normal amplitude) and then curly (a right-handed helix with half the normal pitch and half the normal amplitude). This therefore suggests that the tumbling angle has bidirectionality.
Tumble angleBidirectionalAW405Personal communication with Howard Berg. "The direction is random, more or less, but there is a slight forward bias. It varies from tumble to tumble. The turn-angle distribution peaks at 68 deg rather than 90 deg.

Tumbles turn out to be more complex than believed in 1972. Motors switch independently, and a tumble can occur if one or just a few motors change their directions of rotation. Tumbles are short, as judged by the tracking microscope, because they involve filament physics rather than motor physics: a transformation in polymorphic form, following motor reversal, from normal to semi-coiled."

Tumbling time0.14±0.19sAW405Exponential distribution fitted (stated to be exponential by Berg and Brown) using only the mean tumble length (not STDEV).
Relationship between tumbling angle and time
Speed while Tumbling0μm/sAW405Berg and Brown noted that AW405 slowed/stopped while tumbling.
Isotropic run lengths0.86±1.18sAW405Exponential distribution fitted, this is only an approximate and does not fit exactly (see fig.4 Berg and Brown) The standard deviation is the standard deviation of the mean and has not been used in the exponential distribution
Drift during runAW405Drift was observed. It is what would be expected from rotational diffusion. (at 2.7cp at 32ºC drift was 23±23°). Rotational Brownian motion cause the cell to veer off course, so that in between tumbles the probability density function f of the swimming direction e evolves according to the Fokker-Planck equation. Drift velocity in steep gradient of attractant ~7 µm/s (Berg & Turner, 1990)






No modelling has been carried out yet.

Models

No modelling has been carried out yet.

GRN Models

Agent Based

Hybrid

Results

Modelling Photo Album



Retrieved from "http://2008.igem.org/Team:BCCS-Bristol/Modeling"