Team:BCCS-Bristol/Modeling
From 2008.igem.org
(→25/07/08) |
(→Progress) |
||
| Line 22: | Line 22: | ||
== Approach == | == Approach == | ||
== Progress == | == Progress == | ||
| - | |||
| - | |||
| + | === 16th - 23rd July === | ||
| + | • Implemented run & tumble motion | ||
| - | + | • With/without chemotaxis | |
| - | + | ||
| + | • Implemented interactions between objects (bacteria and particles) | ||
| + | Run and tumble motion | ||
| - | + | A fairly realistic model of bacterial motion; bacterial motion consists of two phases: | |
| - | + | ||
| + | • The run; movement in a straight line. Speed is constant and equal for all bacteria | ||
| + | • The tumble; stationary rotation | ||
| - | + | All parameters are determined at the start of the respective phase. | |
| - | + | The run time is sampled by feeding a random number in the range [0, 1] to an inverse | |
| + | exponential function, with parameters found from the literature. | ||
| + | Tumble time and tumble angle are determined independently, as tumbles can occur at | ||
| + | different speeds due to the independent nature of the flagella motors. Tumble time is | ||
| + | gamma-distributed, and determined in the same way as run length; tumble angle is | ||
| + | sampled from a fourth-order polynomial approximation of an inverse gamma | ||
| + | distribution. The tumble angle is bi-directional, with an equal probability of clockwise or | ||
| + | anticlockwise tumbles; however, there is a slight forward bias – i.e. the mean angle is | ||
| + | less than 90 degrees. | ||
| - | + | ==== Chemotaxis ==== | |
| + | The chemotactic gradient has an effect on the mean run length of a bacterium; runs up | ||
| + | the gradient have a longer mean length. A chemotactic gradient can therefore be | ||
| + | simulated by sampling run length from one of two exponential distributions with | ||
| + | different means, depending on the direction of movement. Using a single distribution | ||
| + | for run length regardless of direction corresponds to the isotropic case, where no | ||
| + | chemotactic gradient is in place. | ||
| - | === | + | ==== Interactions ==== |
| + | Implementation of interactions required a change in the movement heuristic. The | ||
| + | movement was previously determined by speed and direction. This was substituted in | ||
| + | favour of a force-based physics engine. A bacterium experiences forces due to its own | ||
| + | intended movement, if it is in a run phase, and the reaction forces resulting from | ||
| + | interactions between other objects (bacteria and particles). Particles only experience | ||
| + | reaction forces. For each object, all forces are resolved to determine a single resultant | ||
| + | force with x and y components; this resultant force is used to calculate a velocity using | ||
| + | Stokes’ Law for spheres moving through fluids with low Reynolds numbers. Because the | ||
| + | Reynolds numbers involved are so small (around 10-6), inertia is negligible so | ||
| + | acceleration is ignored and velocity is calculated at each time step independently of the | ||
| + | previous velocity. | ||
| + | === 24th – 30th July === | ||
| - | + | • Adapted gamma distribution for tumble angle | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | • | + | • Added trace to particles, and to the mean position of the bacteria |
| - | • | + | • Changed run length calculation heuristic |
| - | + | ==== Gamma distribution ==== | |
| + | Mario commented that the polynomial approximation seemed to result in greater | ||
| + | tumbling angles than those expected from the literature. This problem was resolved | ||
| + | using a database of 1000 pre-computed values derived from the matlab inverse gamma | ||
| + | distribution. | ||
| - | + | ==== Object tracing ==== | |
| + | Whilst watching the simulations we noticed that is hard to follow a particles path; we | ||
| + | therefore added tracers, with a colour gradient representing time, to the particle. The | ||
| + | positions of the particles over time are stored in a database. This could be used for | ||
| + | statistical analysis in future. | ||
| - | + | We also trace the mean position of all bacteria over time to observe any emergent | |
| - | + | behaviour. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | ==== Run Length calculation ==== | ||
| + | Previously the run length was determined at the start of each run. To allow chemotactic | ||
| + | behaviour over more complex chemical fields, a Bernoulli Process was implemented | ||
| + | instead; during a run, at each time step there is a fixed probability that the run will be | ||
| + | terminated. The probability takes one of three values, depending on the bacterium’s | ||
| + | perception of the chemoattractant. The three cases are: | ||
| + | • If the bacterium is unable to detect a change in chemoattractant concentration it | ||
| + | perceives itself to be in an isotropic environment. This occurs when the | ||
| + | concentration change of the chemoattractant is below a sensitivity threshold. | ||
| + | • A perceived increase in chemoattractant concentration will result in a lower run | ||
| + | termination probability. | ||
| + | • A perceived decrease in chemoattractant will result in a higher run termination | ||
| + | probability. | ||
| + | === 31st July – 5th August === | ||
| + | • Implemented wrapping boundaries | ||
| + | • Written a class that allows parameters to be altered whilst the program is | ||
| + | running | ||
| + | ==== Wrapping boundaries ==== | ||
| + | New class was implemented to limit the diffusion of bacteria in the simulation space. A | ||
| + | wrapping boundary consists of a line and an offset vector. When an object touches the | ||
| + | line its position is changed according to the offset vector. These can be used to simulate | ||
| + | a continuous stream of bacteria past an area of interest (the neighbourhood of the | ||
| + | particles), whilst only computing the movement of a small number of bacteria. | ||
| - | + | ==== Run-time parameter control ==== | |
| - | + | Previously all parameters were ‘hardwired’ into the program, meaning that they had to | |
| + | be changed by hand before the simulation was run. A new parameters class was | ||
| + | constructed that allows us to change parameters whilst the program is running, enabling | ||
| + | us to run batches of simulations for statistical analysis. A GUI was also added so that the | ||
| + | user can change parameters without needed to alter the code. | ||
== Models == | == Models == | ||
Revision as of 15:30, 8 August 2008
  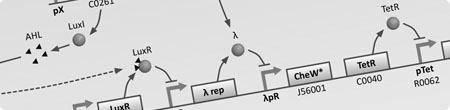
|
Contents |
Approach
Progress
16th - 23rd July
• Implemented run & tumble motion
• With/without chemotaxis
• Implemented interactions between objects (bacteria and particles) Run and tumble motion
A fairly realistic model of bacterial motion; bacterial motion consists of two phases:
• The run; movement in a straight line. Speed is constant and equal for all bacteria
• The tumble; stationary rotation
All parameters are determined at the start of the respective phase. The run time is sampled by feeding a random number in the range [0, 1] to an inverse exponential function, with parameters found from the literature. Tumble time and tumble angle are determined independently, as tumbles can occur at different speeds due to the independent nature of the flagella motors. Tumble time is gamma-distributed, and determined in the same way as run length; tumble angle is sampled from a fourth-order polynomial approximation of an inverse gamma distribution. The tumble angle is bi-directional, with an equal probability of clockwise or anticlockwise tumbles; however, there is a slight forward bias – i.e. the mean angle is less than 90 degrees.
Chemotaxis
The chemotactic gradient has an effect on the mean run length of a bacterium; runs up the gradient have a longer mean length. A chemotactic gradient can therefore be simulated by sampling run length from one of two exponential distributions with different means, depending on the direction of movement. Using a single distribution for run length regardless of direction corresponds to the isotropic case, where no chemotactic gradient is in place.
Interactions
Implementation of interactions required a change in the movement heuristic. The movement was previously determined by speed and direction. This was substituted in favour of a force-based physics engine. A bacterium experiences forces due to its own intended movement, if it is in a run phase, and the reaction forces resulting from interactions between other objects (bacteria and particles). Particles only experience reaction forces. For each object, all forces are resolved to determine a single resultant force with x and y components; this resultant force is used to calculate a velocity using Stokes’ Law for spheres moving through fluids with low Reynolds numbers. Because the Reynolds numbers involved are so small (around 10-6), inertia is negligible so acceleration is ignored and velocity is calculated at each time step independently of the previous velocity.
24th – 30th July
• Adapted gamma distribution for tumble angle
• Added trace to particles, and to the mean position of the bacteria
• Changed run length calculation heuristic
Gamma distribution
Mario commented that the polynomial approximation seemed to result in greater tumbling angles than those expected from the literature. This problem was resolved using a database of 1000 pre-computed values derived from the matlab inverse gamma distribution.
Object tracing
Whilst watching the simulations we noticed that is hard to follow a particles path; we therefore added tracers, with a colour gradient representing time, to the particle. The positions of the particles over time are stored in a database. This could be used for statistical analysis in future.
We also trace the mean position of all bacteria over time to observe any emergent behaviour.
Run Length calculation
Previously the run length was determined at the start of each run. To allow chemotactic behaviour over more complex chemical fields, a Bernoulli Process was implemented instead; during a run, at each time step there is a fixed probability that the run will be terminated. The probability takes one of three values, depending on the bacterium’s perception of the chemoattractant. The three cases are:
• If the bacterium is unable to detect a change in chemoattractant concentration it perceives itself to be in an isotropic environment. This occurs when the concentration change of the chemoattractant is below a sensitivity threshold.
• A perceived increase in chemoattractant concentration will result in a lower run termination probability.
• A perceived decrease in chemoattractant will result in a higher run termination probability.
31st July – 5th August
• Implemented wrapping boundaries
• Written a class that allows parameters to be altered whilst the program is running
Wrapping boundaries
New class was implemented to limit the diffusion of bacteria in the simulation space. A wrapping boundary consists of a line and an offset vector. When an object touches the line its position is changed according to the offset vector. These can be used to simulate a continuous stream of bacteria past an area of interest (the neighbourhood of the particles), whilst only computing the movement of a small number of bacteria.
Run-time parameter control
Previously all parameters were ‘hardwired’ into the program, meaning that they had to be changed by hand before the simulation was run. A new parameters class was constructed that allows us to change parameters whilst the program is running, enabling us to run batches of simulations for statistical analysis. A GUI was also added so that the user can change parameters without needed to alter the code.
Models
No modelling has been carried out yet.
GRN Models
Agent Based
Hybrid
Results
Modelling Photo Album
|
|
 "
"