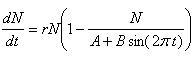Team:NTU-Singapore/Parts/Parameter Estimation using Characterization Results
From 2008.igem.org
Lalala8585 (Talk | contribs) |
Lalala8585 (Talk | contribs) (→Logistic Growth Model with Varying Carrying Capacity) |
||
| Line 41: | Line 41: | ||
===Logistic Growth Model with Varying Carrying Capacity=== | ===Logistic Growth Model with Varying Carrying Capacity=== | ||
| - | [[Image: | + | [[Image:Log_sin1.JPG|200px| Logisitic sine Growth equation]] [[Image:Logistic_VCC1.jpg|700px| Logisitic Growth Model]] <br> |
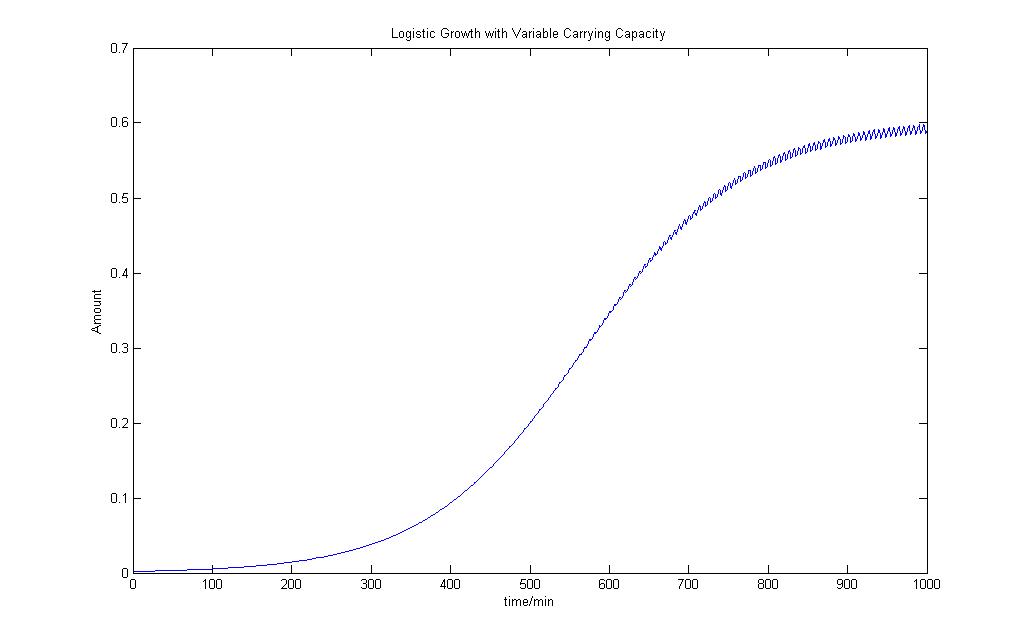
From the model, we can see that population that has an early exponential phase of growth and is not so affected by the variability in the carrying capacity. As the population reaches the limit, the population starts to oscillate at the same frequency as the carrying capacity and some of the population starts to die off. | From the model, we can see that population that has an early exponential phase of growth and is not so affected by the variability in the carrying capacity. As the population reaches the limit, the population starts to oscillate at the same frequency as the carrying capacity and some of the population starts to die off. | ||
We would use this as our logisitc equation model to add a bit more variability into our deterministic model. | We would use this as our logisitc equation model to add a bit more variability into our deterministic model. | ||
| - | + | ||
===Complex Formation=== | ===Complex Formation=== | ||
In an ODE model, a reaction network is expressed as a set of differential equations with one equation per chemical and with terms that represent the reactions. Our complex formation equation has ignored the fact that the reaction could be reversible. Here we add in a new complex formation equation to make our models more robust. | In an ODE model, a reaction network is expressed as a set of differential equations with one equation per chemical and with terms that represent the reactions. Our complex formation equation has ignored the fact that the reaction could be reversible. Here we add in a new complex formation equation to make our models more robust. | ||
Revision as of 05:54, 30 August 2008
|
Contents |
Lactose Induced GFP production
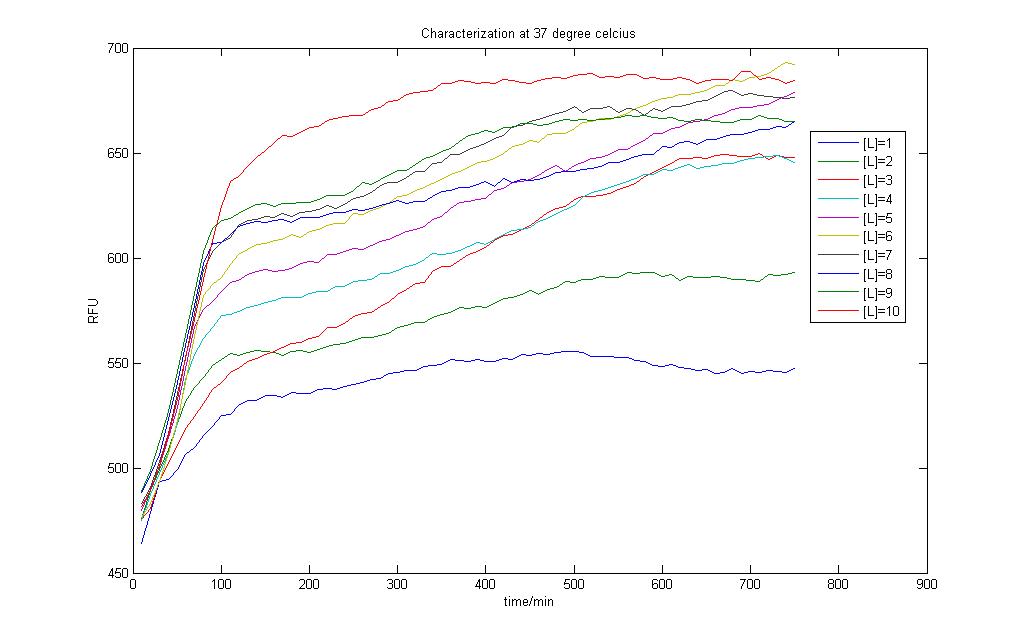
In the above two figures, we have a comparison between the model generated by our very own equations versus the RFU results that we have obtained using our characterization procedures. There are certain features that are our outstanding when these two figures are compared.
1)The deterministic model has not captured any of the stochastic features the real situation presented before us. 2)The model seems to hit steady state much faster than the actual situation
Careful observation of the results from the characterisation and one would notice that the output takes on the form of a sigmoid curve. Indeed, one of the major flaws in our modeling exercise was that the models don't account for cell growth. Even though we used M9 medium to do our characterisation, it is impossible to assume the cells don't multiply and grow within the 12 hour time period!
This prompts us to look into a better model such that we can first capture the essentials of the real situation before we decide to use our models with our characterisation results
Creating a Logistic Growth Construct
The logistic growth model is typically applied to growth kinetics of Microbes and other natural phenomena. This phenomena is based on the fact that no population can expand exponentially forever and there will be a certain limit to the number of species based on the space that is available.
Here we explore the results of three Logistic Growth equations and their various outputs to see how well the results turn out to be.
Logistic Growth Model


N = number of species in the population
t = time
Nmax = Maximum number of species in the ecosystem
r = intrinsic rate of natural increase
Logistic Growth Model with lag phase
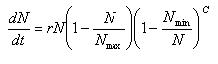

Nmin = Minimum number of species in the ecosystem
c = Adjustment factor
Logistic Growth Model with Varying Carrying Capacity
From the model, we can see that population that has an early exponential phase of growth and is not so affected by the variability in the carrying capacity. As the population reaches the limit, the population starts to oscillate at the same frequency as the carrying capacity and some of the population starts to die off.
We would use this as our logisitc equation model to add a bit more variability into our deterministic model.
Complex Formation
In an ODE model, a reaction network is expressed as a set of differential equations with one equation per chemical and with terms that represent the reactions. Our complex formation equation has ignored the fact that the reaction could be reversible. Here we add in a new complex formation equation to make our models more robust.
Using , and assuming mass action kinetics, the differential equation for C is
kf = forward reaction rate kr = reverse reaction rate
Links
Do refer to Parameter Estimation of GRP production system for more details on the above parameters used.
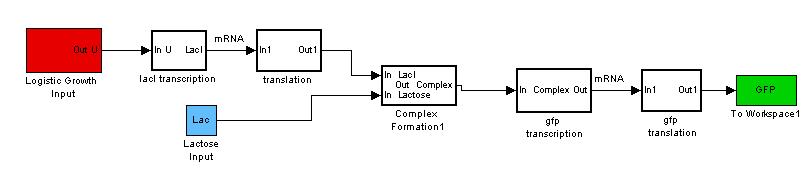
Building the Construct
Revisiting the general idea of our modeling, we have treated each bacteria cell to work as a CSTR (Continuous stirred Reactor).
However, each bacteria is itself a reactor and these "mini reactors" multiply and grow~! Therefore we want our new model to be able to account for both the production of proteins and the growth pattern of the bacteria. So now instead of a simple basal signal into our model, we would send in a signal that codes for a "logistic growth" in the basal transcription of the model.

By giving our reactor model a signal to "grow", we can try to simulate this logistic growth output as observed in our experiments.

As seen, the logistic input can still capture varying lactose inputs and this model seems to be a more representative one for the characterization results. We intend to use these results for our characterization experience and it will be found in the next section.
References
1. A new logistic model for Escherichia coli growth at constant and dynamic temperatures FUJIKAWA Hiroshi ; KAI Akemi ; MOROZUMI Satoshi
 "
"