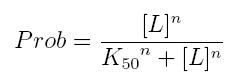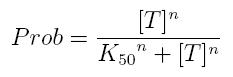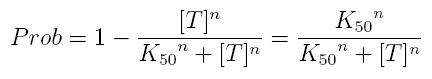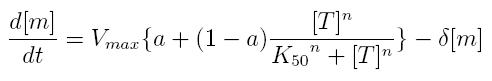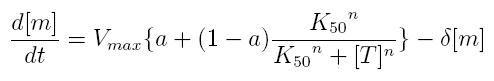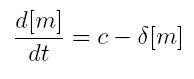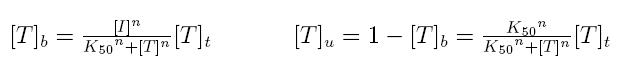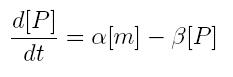Team:UNIPV-Pavia/Modeling
From 2008.igem.org
| Line 142: | Line 142: | ||
In the following paragraphs, the complete ODE systems and the Simulink block diagrams will be reported. | In the following paragraphs, the complete ODE systems and the Simulink block diagrams will be reported. | ||
=== '''Mux'''=== | === '''Mux'''=== | ||
| + | {|cellpadding="1px" align="center" | ||
| + | |[[Image:pv_mux_simulink.jpg|500px|left]] | ||
| + | |} | ||
=== '''Demux'''=== | === '''Demux'''=== | ||
| + | {|cellpadding="1px" align="center" | ||
| + | |[[Image:pv_demux_simulink.jpg|500px|left]] | ||
| + | |} | ||
<br> | <br> | ||
Revision as of 22:47, 29 September 2008
Contents |
Mathematical modeling page
In this section we explain two dynamic models that can be used to describe the gene networks in our project. After a brief overview about the motivation of a mathematical model, we will illustrate the general formulas we used, we will show the complete ODE models for Mux and Demux gene networks, and then we will report results of some simulations performed with Matlab and Simulink.
Why writing a mathematical model?
The purposes of writing mathematical models for gene networks can be:
- Prediction: a good and well identificated model can be used in simulations to predict real system behavior. In particular we could be interested in system output in response to never seen inputs. In this way, the system can be tested 'in silico', without performing real experiments 'in vitro' or 'in vivo'.
- Parameter identification: we already wrote that it is very important to estimate all the parameters involved in the model, in order to perform realistic simulations. Another goal that can be reached with parameter identification is 'network summarization', in fact estimated parameters can be used as 'behavior indexes' for the network (or a part of it). These indexes can be very useful for synthetic biologists to choose and compare BioBrick standard parts for genetic circuits design, just like electronic engineers choose, for example, a Zener diode, knowing its Zener voltage.
Equations for gene networks
In this paragraph, mathematical modeling for gene and protein interactions will be described.
Binding of a ligand to a molecule: Hill equation
The fraction of a molecule saturated by a ligand ( = the probability that the molecule is bound to a ligand) can be expressed as a function of ligand concentration using Hill equation:
- Prob: the probability that the molecule is bound to the ligand
- [T]: concentration of the ligand
- K50: dissociation constant. It is the concentration producing a probability of 0.5
- n: Hill coefficient. It describes binding cooperativity
Regulated transcription
Transcription of a mRNA molecule can be regulated by transcription factors in active form. These factors can be activators or inhibitors: they respectively increase and decrease the probability that RNA polymerase binds the promoter. This probability must be function of active transcription factor concentration and can be modeled using Hill equation. If factor in active form activates transcription, we can write:
- Prob: probability that the gene is transcripted
- [T]: concentration of the transcription activator in active form
- K50: dissociation constant. It is the concentration producing a probability of 0.5
- n: Hill coefficient (n>0)
while, if factor in active form inhibits transcription, we are interested in unbound promoter and so we can write:
- Prob: probability that the gene is transcripted
- [T]: concentration of the transcription inhibitor in active form
- K50: dissociation constant. It is the concentration producing a probability of 0.5
- n: Hill coefficient (n>0)
The equations show that:
- In activation formula, if [T]=0 the trascription probability is Prob=0, while the maximum probability, Prob=1, is reached asymptotically for [T]->Inf
- In inhibition formula, if [T]=0 the trascription probability is Prob=1, while the minimum probability, Prob=0, is reached asymptotically for [T]->Inf
These formulas can be included in a differential equation that can describe the dynamic behavior of a mRNA molecule as a function of the factor that regulates its transcription.
ODE for activated transcription
- Vmax: maximum transcription rate
- [m]: concentration of mRNA molecule
- [T]: concentration of the transcription activator in active form
- K50: dissociation constant
- n: Hill coefficient (n>0)
- delta: mRNA degradation constant
- a: leakage factor that can modellize promoter basic activity. It is a percentage of Vmax
ODE for inhibited transcription
- Vmax: maximum transcription rate
- [m]: concentration of mRNA molecule
- [T]: concentration of the transcription inhibitor in active form
- K50: dissociation constant
- n: Hill coefficient (n>0)
- delta: mRNA degradation rate
- a: leakage factor that can modellize promoter basic activity. It is a percentage of Vmax
ODE for constitutive transcription
- c: constant transcription rate
- [m]: concentration of mRNA molecule
- delta: mRNA degradation rate
Transcription factors in active form
Formulas described so far are dependent on the concentration of transcription factor in active form. But how can we calculate the amount of transcription factor in active form? Assuming that the transcription factor can be activated or inhibited by a inducer factor (that can be an exogenous input), we can use Hill equation again to calculate the concentration of bound and unbound transcription factor as a function of the inducer factor:
- [I]: concentration of the inducer
- [Tt]: total concentration of the transcription factor
- [Tu]: concentration of unbound transcription factor
- [Tb]: concentration of bound transcription factor
- K50: dissociation constant
- n: Hill coefficient (n>0)
If active form is bound transcripion factor, we are interested in Tb, while if active form is unbound transcription factor, we are interested in Tu.
ODE for protein production
We have to modellize translation of mRNA molecules. We chose to describe it as a differential equation in which protein production and protein degradation are linear:
- [P]: concentration of protein
- [m]: concentration of mRNA molecule
- alpha: translation rate
- beta protein degradation rate
Our model
We considered Tetracycline, IPTG, Arabinose and GFP respectively as CH0, CH1, SEL and OUT signals for Mux, while we considered IPTG, Tetracycline, RFP and GFP respectively as IN, SEL, OUT0 and OUT1 signals. For all these signals, logic 1 corresponds to the presence of the molecule.
According to the equations described so far, every protein and mRNA is a state variable for the model. Mux and Demux models are described in the next paragraphs.
We considered dimensionless equations, in which parameters have been calibrated qualitatively, to study system trends and to build up a scaffold for future parameter identification.
In the following paragraphs, the complete ODE systems and the Simulink block diagrams will be reported.
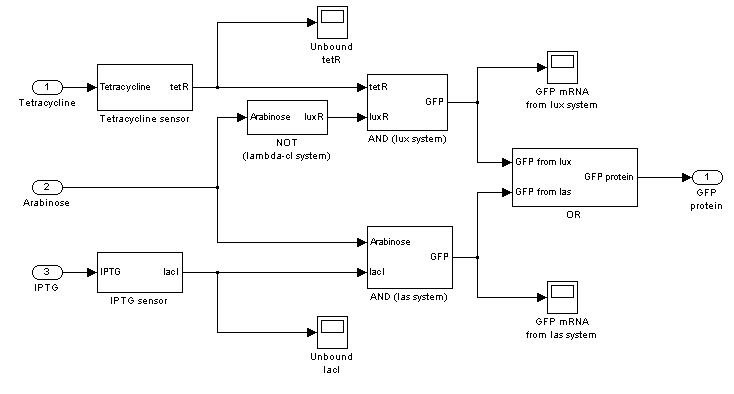
Mux
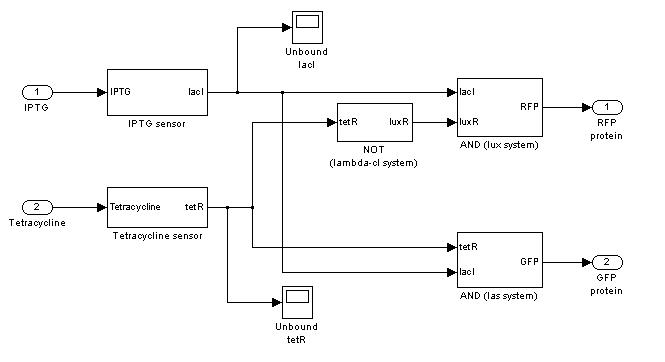
Demux
Simulations
Mux
Demux
References
[1] Modelli multiscala per studi di proteomica e genomica funzionale, S. Cavalcanti, S. Furini, E. Giordano. "Genomica e proteomica computazionale", GNB Book, Publisher: Pàtron, 2007
[2] ETH Zurich iGEM 2007 Wiki - Modeling basics page
 "
"