Team:Imperial College/Motility
From 2008.igem.org
| Line 26: | Line 26: | ||
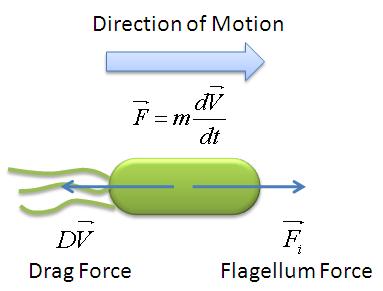
In this model, we attempt to obtain a distribution for the flagellar force, which is represented by parameter ''A''. We assume that the medium is homogenous and the drag coefficient is constant throughout the medium, hence the distribution of flagellar force will be sufficiently be described by parameter A. | In this model, we attempt to obtain a distribution for the flagellar force, which is represented by parameter ''A''. We assume that the medium is homogenous and the drag coefficient is constant throughout the medium, hence the distribution of flagellar force will be sufficiently be described by parameter A. | ||
| + | |||
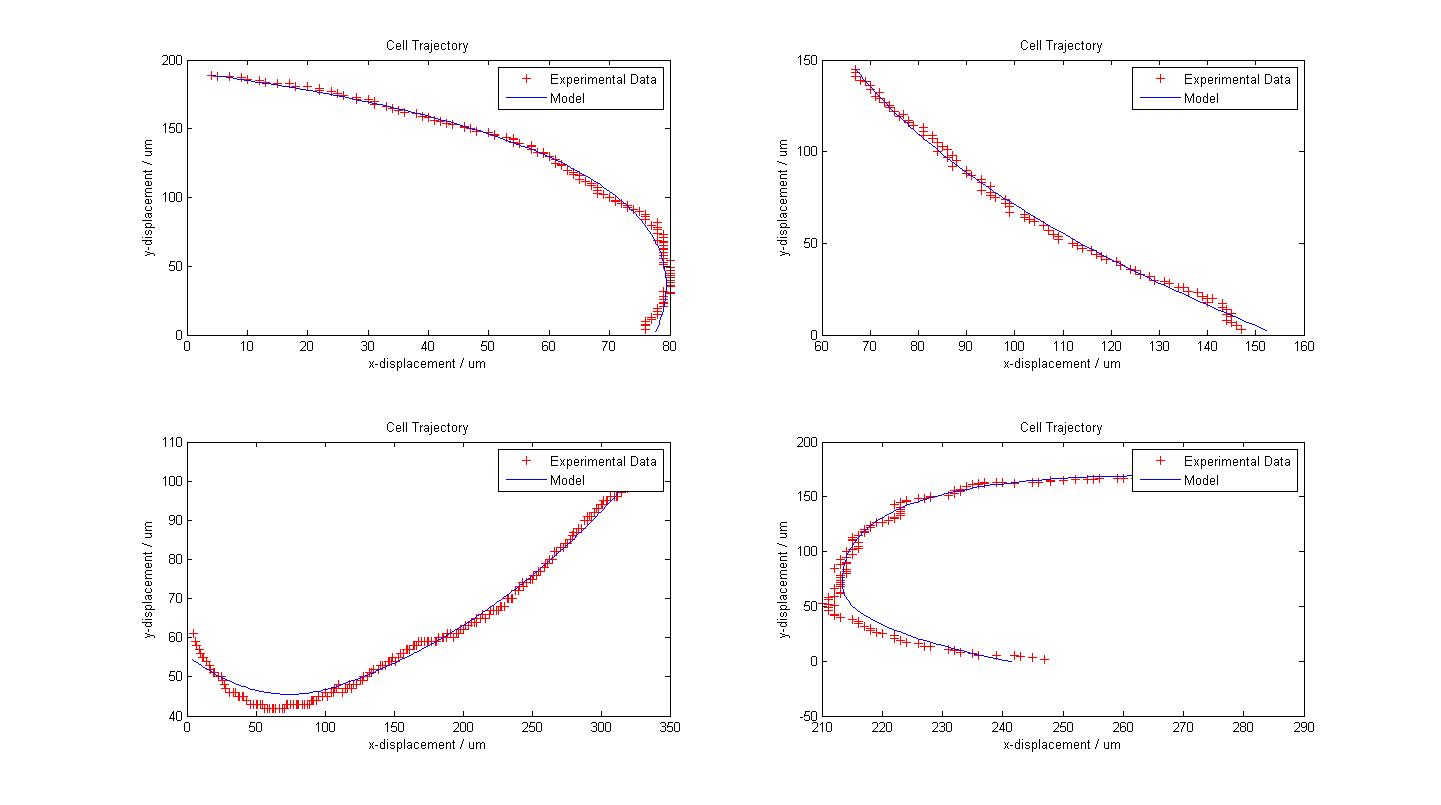
| + | The following figure shows the results of our model fitting. We have introduced a change in flagellar force at certain points of the cell trajectory so as to achieve a better fit. A maximum of two runs were allowed for each cell trajectory. | ||
| + | |||
| + | [[Image:Fitted_Models.jpg|450px|center]]<br> | ||
| + | |||
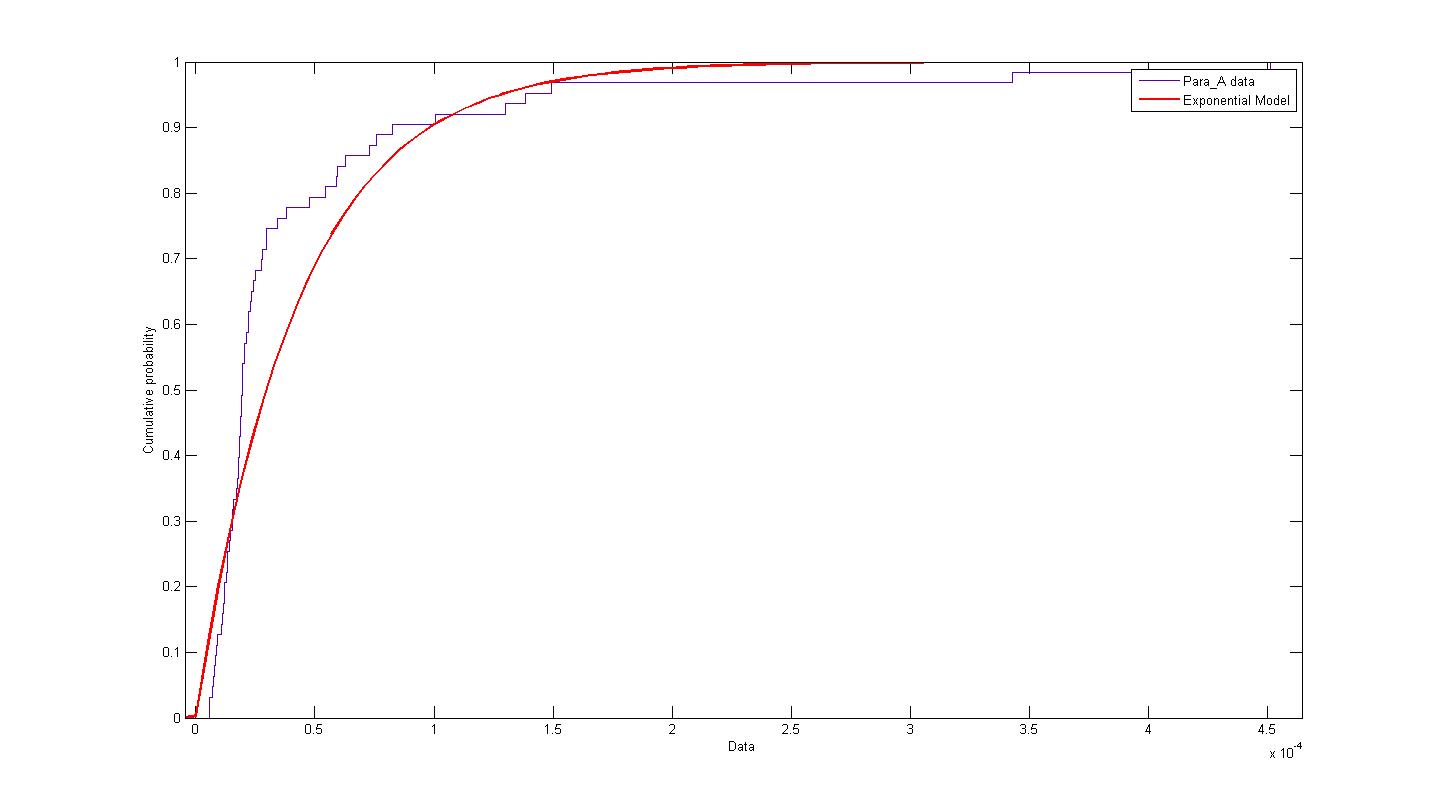
| + | The distribution of parameter A was plotted and modelled according to an exponential model. The following figure describes the probability density function and cumulative density function. | ||
| + | |||
| + | [[Image:Exponential_A_PDF.jpg|450px|center]]<br> | ||
| + | [[Image:Exponential_A_CDF.jpg|450px|center]]<br> | ||
}} | }} | ||
{{Imperial/EndPage|Genetic Circuit|Appendices}} | {{Imperial/EndPage|Genetic Circuit|Appendices}} | ||
Revision as of 11:10, 17 October 2008
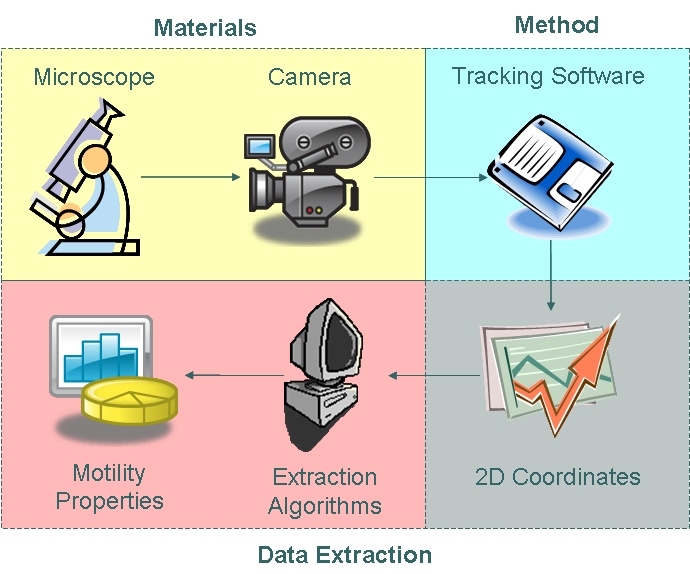
Motility Analysis
|
|||||||
 "
"