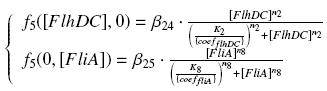Team:Paris/Modeling/f5
From 2008.igem.org
(Difference between revisions)
| Line 9: | Line 9: | ||
[[Image:F5.jpg|center]] | [[Image:F5.jpg|center]] | ||
| - | + | <center> | |
{|border="1" style="text-align: center" | {|border="1" style="text-align: center" | ||
|param | |param | ||
| Line 93: | Line 93: | ||
| | | | ||
|} | |} | ||
| - | + | </center> | |
<br><br> | <br><br> | ||
Revision as of 14:42, 26 October 2008
We have [FlhDC] = {coefflhDC}expr(pTet) = {coefflhDC} ƒ1([aTc]i)
and [FliA] = {coefFliA}expr(pBad) = {coefFliA} ƒ2([arab]i)
So, at steady-states,
| param | signification | unit | value | comments |
| [expr(pFlhDC)] | expression rate of pFlhDC with RBS E0032 | nM.min-1 | need for 20 mesures with well choosen values of [aTc]i and for 20 mesures with well choosen values of [arab]i and 5x5 measures for the relation below? | |
| γGFP | dilution-degradation rate of GFP(mut3b) | min-1 | 0.0198 | |
| [GFP] | GFP concentration at steady-state | nM | need for 20 + 20 measures and 5x5 measures for the relation below? | |
| (fluorescence) | value of the observed fluorescence | au | need for 20 + 20 measures and 5x5 measures for the relation below? | |
| conversion | conversion ratio between fluorescence and concentration | nM.au-1 | (1/79.429) |
| param | signification corresponding parameters in the equations | unit | value | comments |
| β52 | production rate of FlhDC-pFliL with RBS E0032 β52 | nM.min-1 | ||
| (K46/{coeffliA}) | activation constant of FlhDC-pFliL K46 | nM | ||
| n46 | complexation order of FlhDC-pFliL n46 | no dimension | ||
| β53 | production rate of FliA-pFliL with RBS E0032 β53 | nM.min-1 | ||
| (K47/{coefomp}) | activation constant of FliA-pFliL K47 | nM | ||
| n47 | complexation order of FliA-pFliL n47 | no dimension |
Then, if we have time, we want to verify the expected relation
 "
"