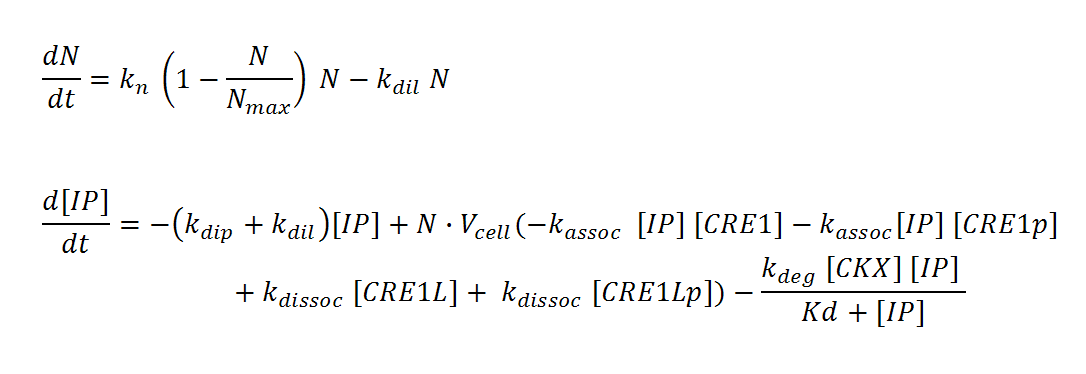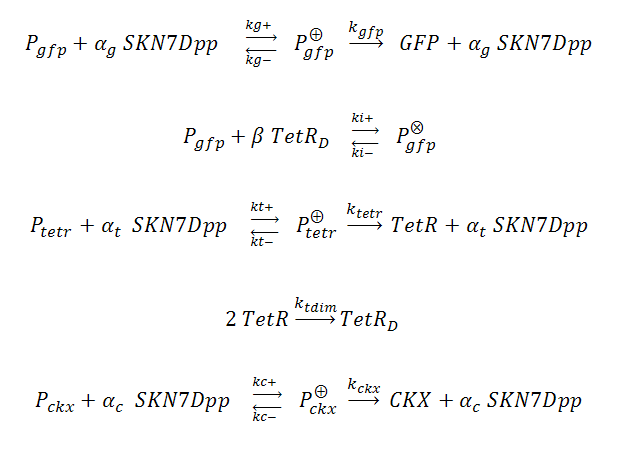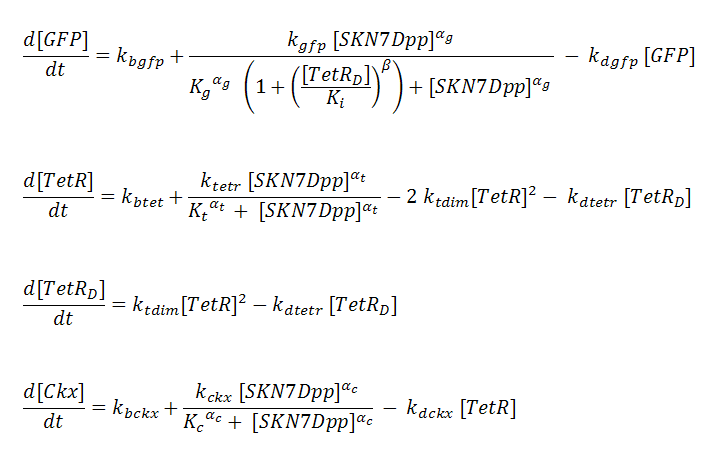Team:University of Ottawa/Modeling
From 2008.igem.org
(→Receiver cells) |
(→Receiver cells) |
||
| Line 138: | Line 138: | ||
Transcription is considered to be rate limiting for gene expression and the kinetics for transcription are modeled as Hill-type. Using the pre-equilibrium assumption for binding of the transcriptional activator SKN7Dpp and repressor TetR to their respective sites on the promoters, we can derive the following equations from the reactions above: | Transcription is considered to be rate limiting for gene expression and the kinetics for transcription are modeled as Hill-type. Using the pre-equilibrium assumption for binding of the transcriptional activator SKN7Dpp and repressor TetR to their respective sites on the promoters, we can derive the following equations from the reactions above: | ||
| - | [[Image: | + | [[Image:GFPeqs.jpg]] |
Revision as of 10:57, 27 October 2008
Modeling
Variables Our models contain the following variables and species:
Reactions
Parameters The values for the parameters governing expression of the core signaling components (IP, CRE1, YPD1, SKN7) were taken from the model of Chen and Weiss []. The parameters specific to our system were either gleaned from other sources if available, or were varied within reasonable ranges to explore their effect on the dynamics of the system.
Receiver cells
N, M and IP are total culture variables. Cell density (N, M) is modeled as logistic growth, with carrying capacity Nmax, Mmax. Continuous culture dilution may be chosen rather than batch culture by setting a nonzero dilution rate (kdil). Inducer concentration (IP) in the reactor is affected by an overall degradation rate (kdip), the culture dilution rate (kdil), and binding/releasing of the molecule to the receptor in both its phosphorylated (CRE1p) and non-phosphorylated (CRE1) state. IP is assumed to diffuse rapidly across the cell membrane so that intracellular and total culture IP concentrations are the same at all times. The effective “receptor concentration” in the total reactor volume (mol receptors/culture volume) is estimated by multiplying the cellular concentration of receptors (mol receptors per cell/cell volume) by the cell density times cell volume. Simple Michaelis-Menten kinetics is used to model enzyme-mediated degradation of IP by CKX. With these assumptions, we derive the differential equations below.
It is assumed that IP binds CRE1 with 1:1 stoichiometry. Ligand-bound CRE1 autophosphorylates and transfers its phosphate to the second messenger YPD1. The response protein SKN7 forms a dimer SKN7D. SKN7D is phosphorylated twice via reversible phosphor-transfer by YPD1. The double phosphorylated SKN7Dpp is the active transcription factor. The differential equations are adapted from Chen and Weiss []; the kinetics for the reactions are approximated using elementary mass action kinetics. These equations represent the changes in a single cell of the population. More precisely, they represent the single cell dynamics averaged over the whole population.
In our system, three genes are under the control of SKN7Dpp: the gene of interest (GFP) is expressed fastest, followed by expression of the TetR repressor, which dimerizes and binds to tet operator (tetO) elements upstream of the GFP cassette, inhibiting its expression and thus creating a “pulse” of GFP. Meanwhile, the product of the third SKN7-induced gene, cytokinin dehydrogenase (CKX), accumulates and degrades IP in the culture, allowing the system to reset itself for another pulse. The GFP, TetR and CKX genes are regulated by different promoters each possessing synthetic SKN7 response elements (SSRE).
P_^⨁ represents the activator-bound promoter, while P_^⨂ represents repressor-bound promoter. TetR binding is assumed to block access of SKN7Dpp to the promoter. Transcription is considered to be rate limiting for gene expression and the kinetics for transcription are modeled as Hill-type. Using the pre-equilibrium assumption for binding of the transcriptional activator SKN7Dpp and repressor TetR to their respective sites on the promoters, we can derive the following equations from the reactions above:
 "
"