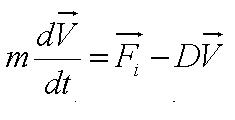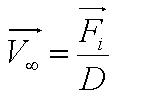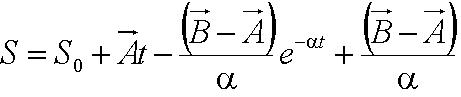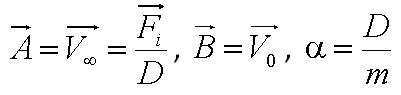Team:Imperial College/Motility
From 2008.igem.org
| Line 42: | Line 42: | ||
{{Imperial/Box1|Results| | {{Imperial/Box1|Results| | ||
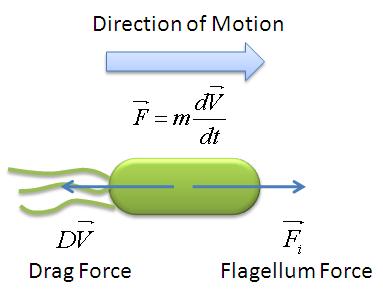
| + | During the model fitting process, we modelled the motility of ''B. subtilis'' to have a maximum of two runs. We keep the value of parameter <math>/alpha</math> constant since it is a ratio of the drag coefficient to the mass. We then let the final velocity of the cell's first run to be equivalent to parameter ''B'', initial velocity of the cell's second run. | ||
| + | |||
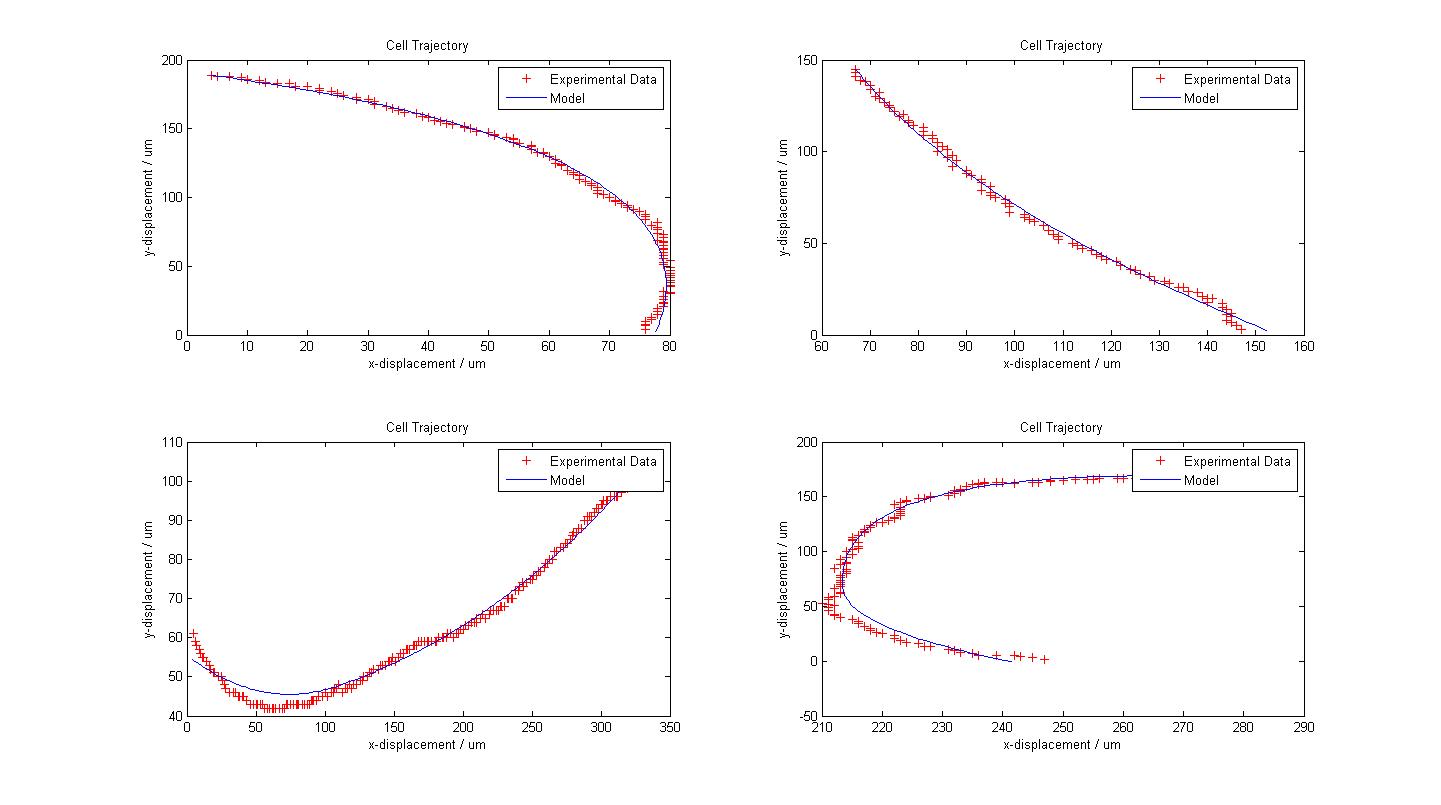
The following figure shows the results of our model fitting. We have introduced a change in flagellar force at certain points of the cell trajectory so as to achieve a better fit. A maximum of two runs were allowed for each cell trajectory. | The following figure shows the results of our model fitting. We have introduced a change in flagellar force at certain points of the cell trajectory so as to achieve a better fit. A maximum of two runs were allowed for each cell trajectory. | ||
Revision as of 18:32, 27 October 2008
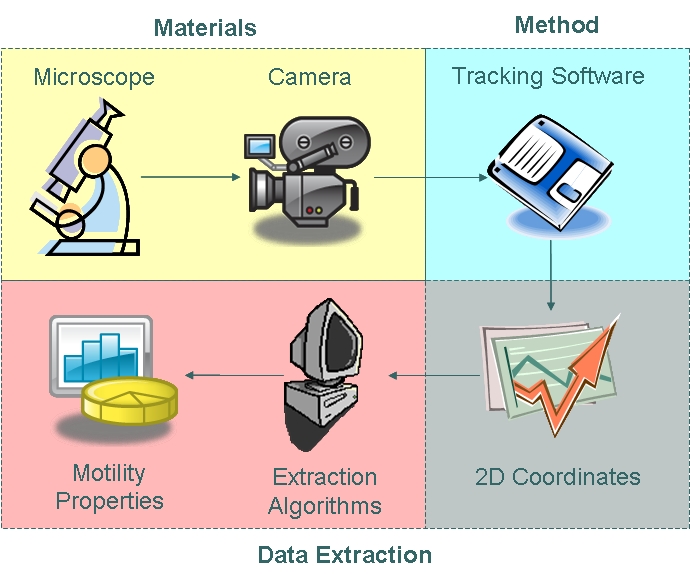
Motility Analysis
|
|||||||||||||||
 "
"