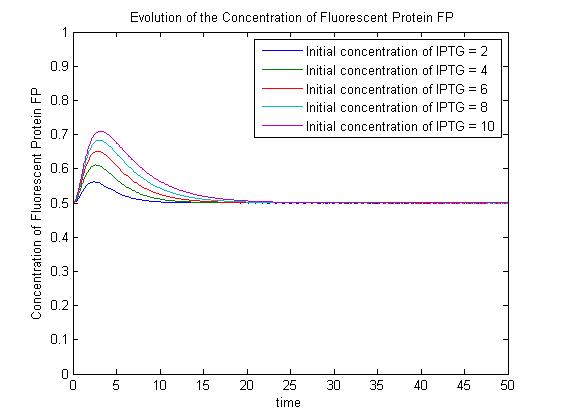
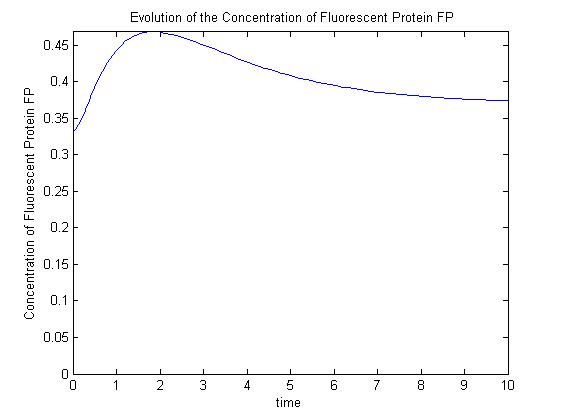
|
A simple synthesis-degradation model is assumed for the modelling of the expression of a protein under the control of a constitutive promoter, with the same model assumed for all four promoter-RBS constructs. The synthesis-degradation model assumes a steady state level of mRNA.
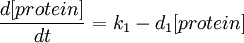
In this case, [protein] represents the concentration of GFP, k1 represents the rate of sythesis and d1 represents the degradation rate.
We can easily simulate this synthesis-degradation model using matlab:
ODE
Simulation File
We can also solve this ODE analytically.
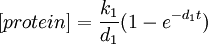
Consider the steady-state behaviour of [protein].

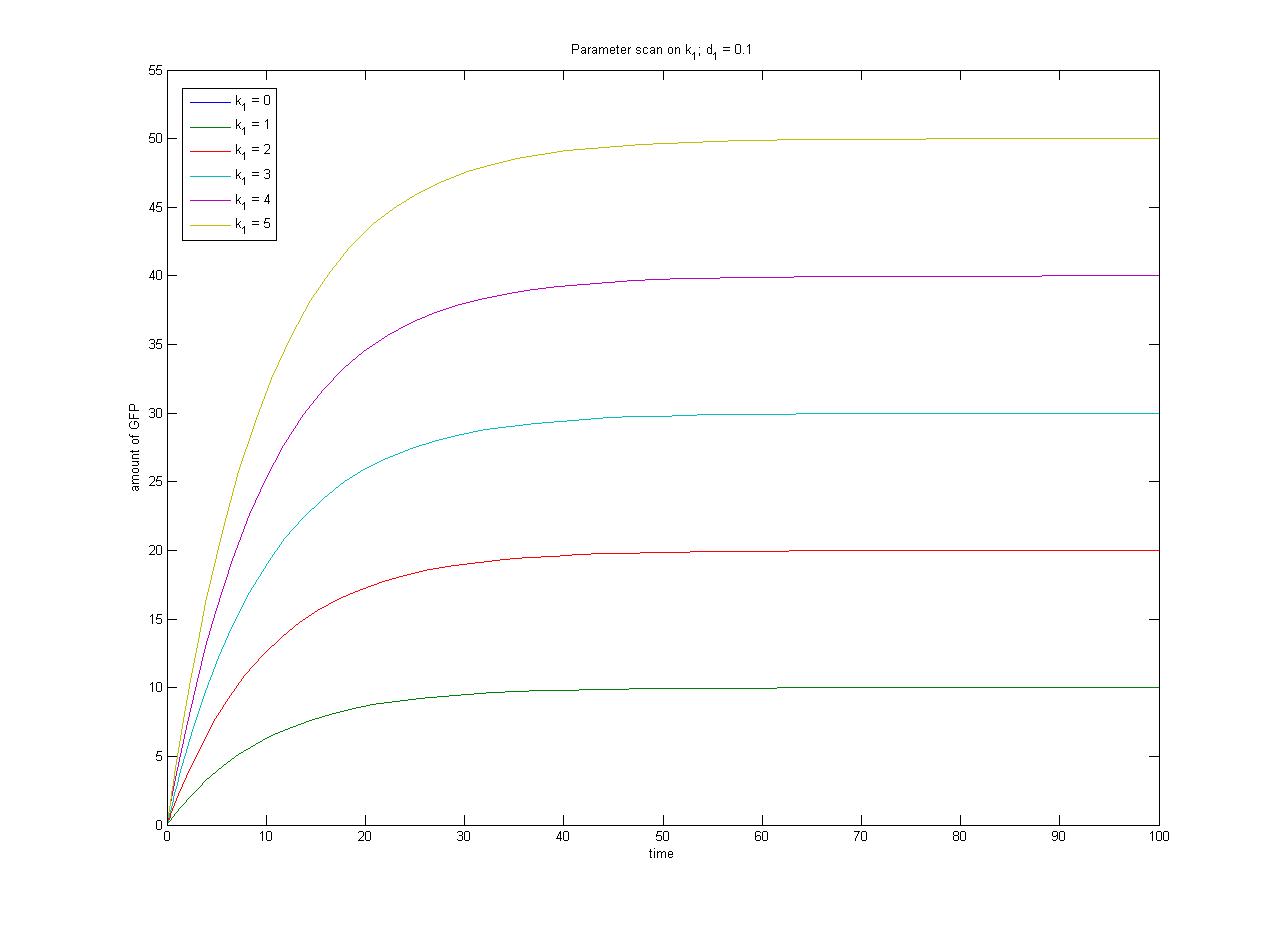
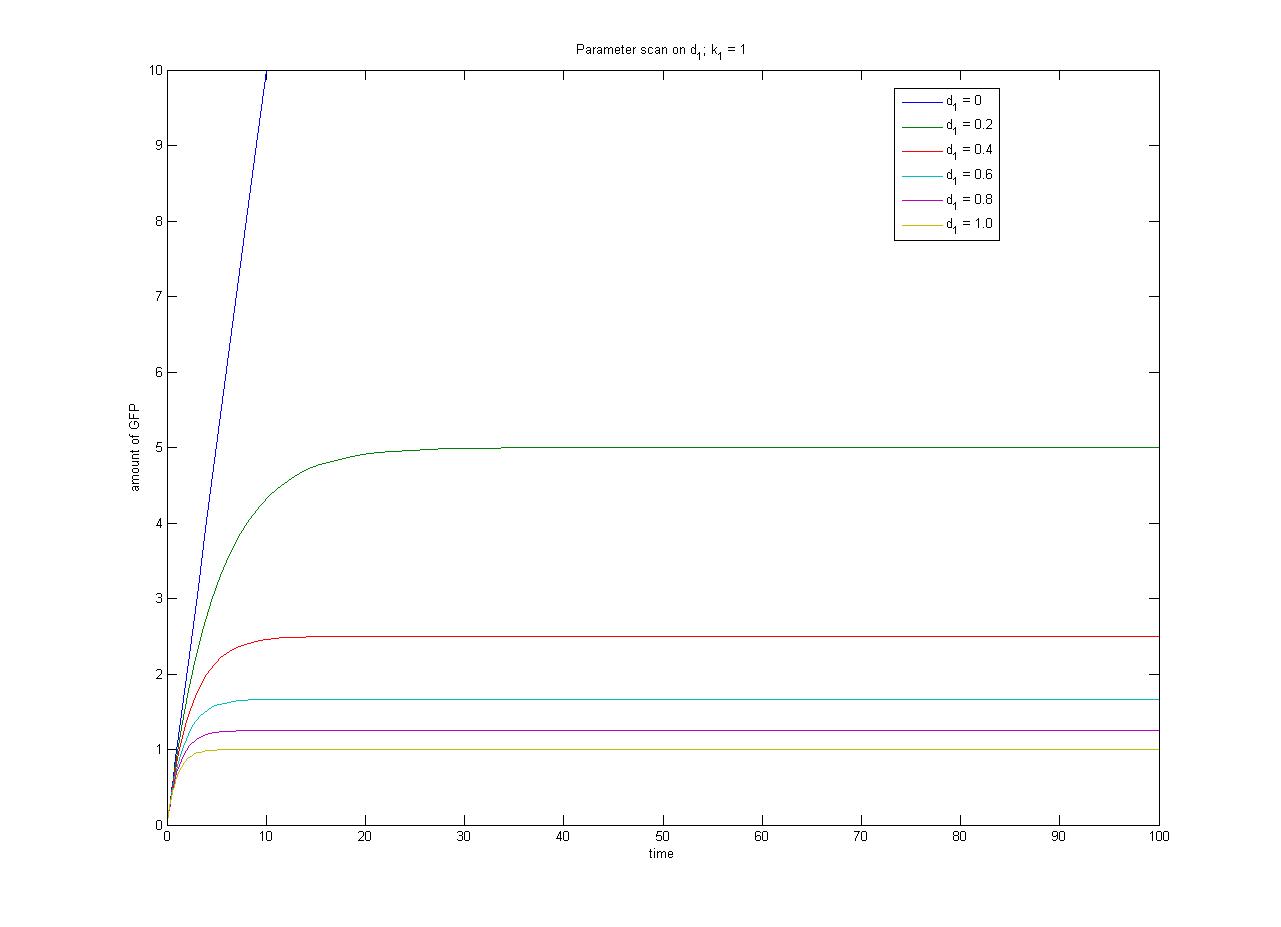
The relationship between the steady-state protein concentration and the parameters can be seen in the parameter scan graphs on the right.
Note from the parameter scan graphs:
- In the case where k1 = 0, no GFP is sythesised.
- In the case where d1 = 0, the concentration of protein does not reach a steady state.
From the wetlab experiments it is likely that we will obtain steady-state data for each of the four promoter-RBS constructs. If we assume the same rate of degradation of GFP in each case, we can use the relative steady-state levels of GFP as a proxy for the relative rate of transcription through each promoter. This will help us with the selection of the most appropriate promoter to use for Phase 2. In order to obtain an absolute measure of transcription (as opposed to a relative measure of transcriptional strength) we require constitutive expression in terms of molecules per cell (as opposed to fluorescence in arbitrary units).
Complementary experiments to estimate the rate of degradation of GFP - by terminating transcription - would allow us to estimate absolute rate of transcription through each promoter.
|  "
"