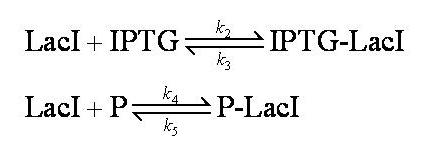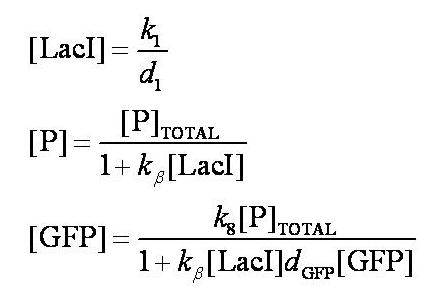Team:Imperial College/Genetic Circuit Details

From 2008.igem.org

(Difference between revisions)
Line 23: Line 23:
To describe the change in concentration of the interacting species over time we used the following system of differential equations:
To describe the change in concentration of the interacting species over time we used the following system of differential equations:
-
[[Image:Simple_model_ODEs.jpg|500px]]
 
-
These are evaluated numerically using Matlab's ODE solver.
 
-
Note from the differential equations above that the steady-state concentration of free promoter (when d[P]/dt=0) will be independent of the concentration of IPTG introduced into the system. The pre-steady-state maximum concentration of GFP attained will differ, however - this is illustrated on the [[Genetic_Circuits|Genetic Circuits]] and can be explored further using the [[Media:insert link here|matlab simulations]]
+
 
}}
}}

Revision as of 00:10, 29 October 2008


Simple Model (1)

Equilibria

Interactions between IPTG, LacI and free promoter and the formation of the promoter-LacI and IPTG-LacI complexes are described using the following equilibria.

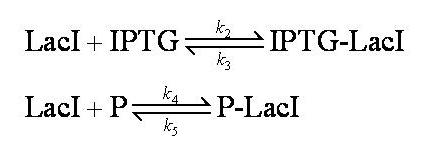
Simple model equilibria.jpg

Note: 1:1 stoichiometry has been assumed; this model could be adapted to use different stoichiometric coefficients.

k2, k3, k4 and k5 represent binding constants for formation and dissociation of complexes.

Equations

Before IPTG is introduced the system is at steady-state. The steady-state levels of LacI, free promoter, and GFP are given by:

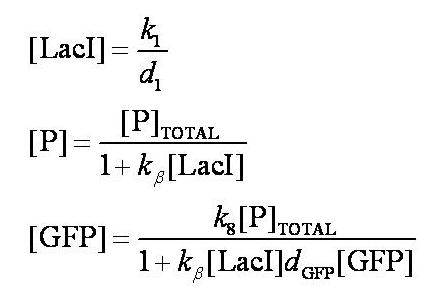
Simple model steady state pre induction.jpg

Note: k1 and k8 represent the rate of transcription through the constitutive promoter upstream of LacI and the promoter upstream of GFP respectively.

d1 and dGFP represent the degradation rates of LacI and GFP respectively.

k_beta is defined as k4/k5.

To describe the change in concentration of the interacting species over time we used the following system of differential equations:




More Sophisticated Model(2)

Equilibria

Assumptions:

No intermediary P-IPTG-LacI complex is formed.

We assumed 2 LacI molecules bind to the promoter.

Equations

Qualitative effect of parameters on behaviour

References
  1. Kuhlman T, Zhang Z, Saier MH Jr, & Hwa T (2007) Combinatorial transcriptional control of the lactose operon of Escherichia coli. - PNAS 104 (14) 6043-6048
  2. Alon, U (2006) An Introduction to Systems Biology: Design Principles of Biological Circuits - Chapman & Hall/Crc Mathematical and Computational Biology


Retrieved from "http://2008.igem.org/Team:Imperial_College/Genetic_Circuit_Details"