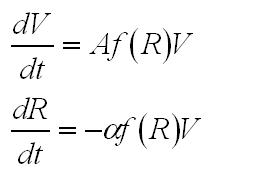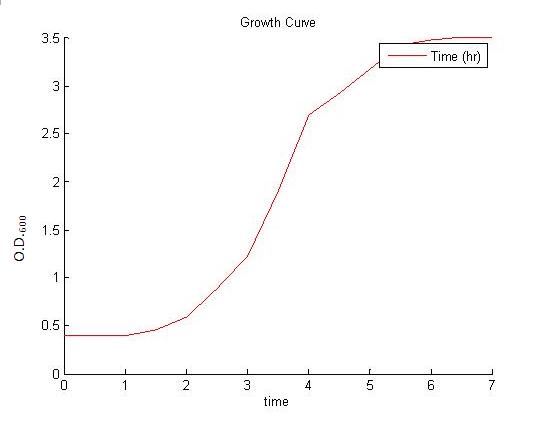
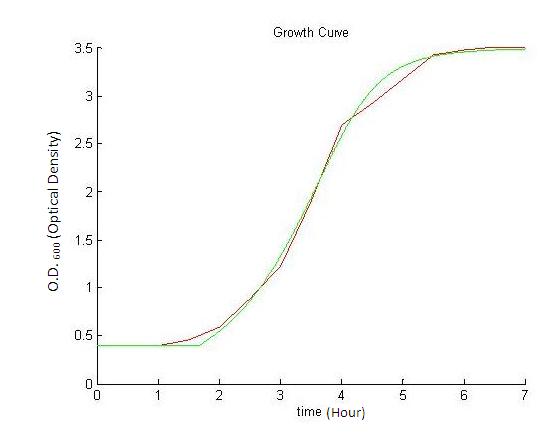
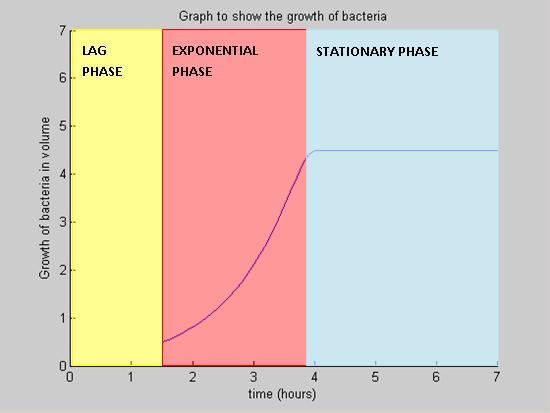
Team:Imperial College/Growth Curve

Part of our dry lab team concentrated on modelling the growth curve of B. subtilis. This is important to characterise the chassis; particularly, the growth of subtilis is a vital parameter for planning experiments for future projects. Characterisation increases the predictability of the growth of B. subtilis by determining, for example, its growth rate and the duration of its distinctive growth phases. In order to model the growth of B. subtilis, the process was broken down into three main steps, where a separate submodel is produced in MATLAB for each step. Each submodel is an ODE model, which can be simulated using MATLAB. The variables in each submodel can be adjusted according to the boundary conditions (from experimental results).

In the final step, a combination of Submodels 1 and 2 are superimposed with Submodel 3, resulting in a more complex model which enhances the accuracy of illustrating bacterial growth. For more details about the submodels, please see the Dry Lab Appendices page.

The graph on the right shows the log graph used to determine the growth rate.

The model illustrates the main growth phases the B. subtilis undergoes. These are identified as the lag phase, the exponential phase and the stationary phase. The death phase is a constitutive event and it is possible that it exerts an influence on the three phases discussed below. However, to simplify a complicated model, it is less relevant in this case and therefore is not included in this model.

Lag Phase

During the lag phase, the rate of growth is slow. All nutrients are situated outside the cell initially. Some time is needed for an adequate amount of nutrients to move from the outside of the cell into the interior of the cell. This is vital as the cell requires the nutrients for growth.

Exponential Phase

Nutrients are consumed during the cell growth and the growth is exponential as long as there are enough nutrients available. The exchange of nutrients ensures that the intra- and extracellular nutrient concentration are the same.

Stationary Phase

The growth of the colony ceases in number and in volume. This happens when the colony has consumed all available nutrients. Other contributing factors may be death and cell division.









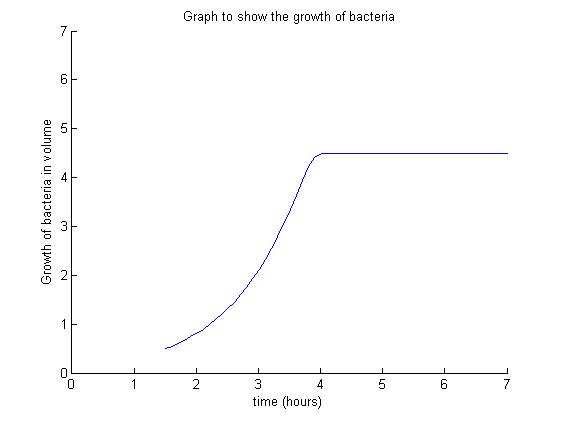
The growth is represented in terms of volume. By doing so we can, to some extent, overlook the process of cell division during the bacteria growth. We can assume the internal concentration of nutrients is reset almost instantaneously to the external concentration. During this time, the total volume does not change.

The growth of the overall volume V is therefore modelled as:

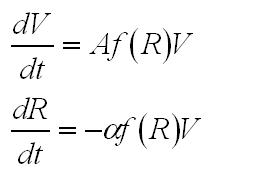
The M-file used to generate the model below is located in the Appendices section of the Dry Lab hub.

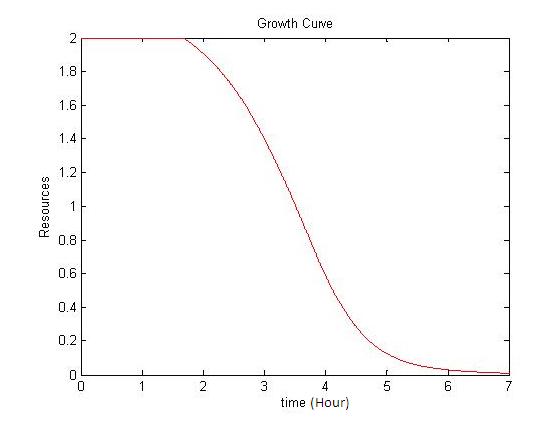
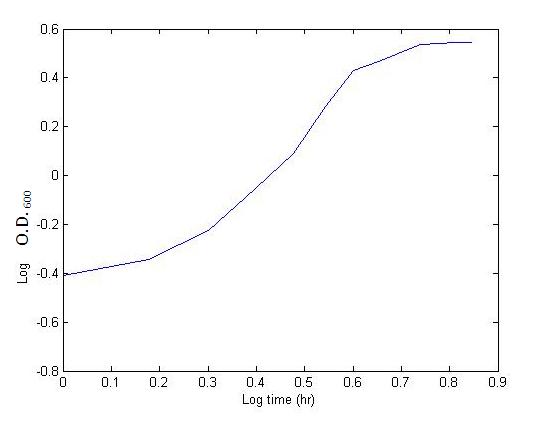
Below is a typical model used for modelling the growth of bacteria. A high growth rate, as illustrated by the model below, will cause nutrients to be uptaken quickly resulting in a 'nutrient crash'. As the amount of resources are limited, the growth curve eventually become flat in the stationary phase. This is when the growth of the bacteria ceases.

The model for the growth curve was fitted to the experimental results. The results are shown below. The experimental results are depicted by the red curve, while our model is shown by the green curve. The resource curve was also plotted as a function of time and is shown below.

The model 'fit' is very good in the exponential and stationary phases. However, this does not apply to the lag phase. This suggests that the model should be expanded in order to take into account phenomena such as the movement of the nutrients into the cells.

Experimental Results	Fitted Curve	Resource Curve

The search for the optimal model parameters was done by brute force. But instead of browsing the whole space of parameters, we reduced the search volume with a simple pre-processing of the experimental data. The initial volume was estimated from the data - likewise the volume in the stationary phase which is directly related to the model parameters R0 and alpha. The model parameter A being related to the apparent growth rate of the experimental data, We plotted the log graph to determine the growth rate of our data.

The following constants were found to yield the best fit to experimental results:
- GROWTH CONSTANT (A): 1.3494
- INITIAL NUTRIENT CONCENTRATION (R₀): 2
- HILL COEFFICIENT (n): 1.25
- INITIAL OD: 0.4
- CONSTANT (α): 0.64516