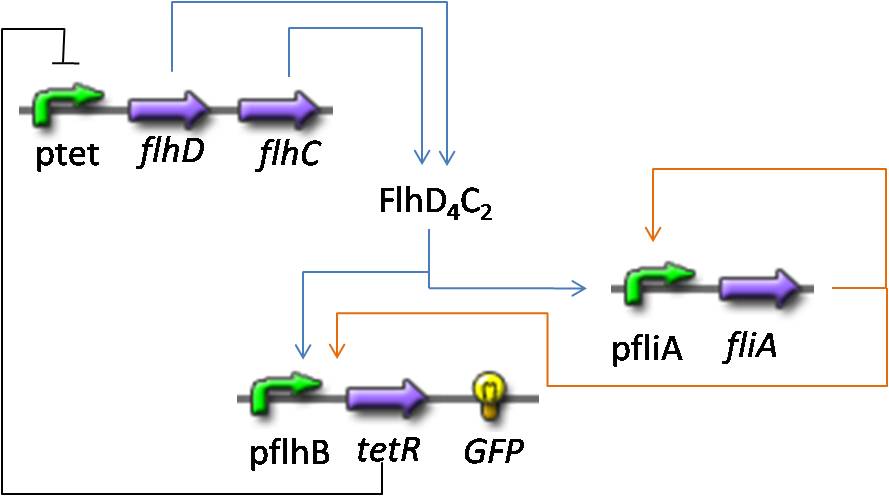
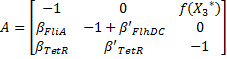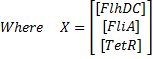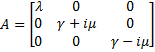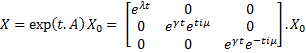(Under Construction : synchronisation and whole system)

Oscillations

Short System

• We wanted to see if, from a mathematical point of view, it was possible for the "short" system presented above to hover.

• Here are the equations we took into account :

• The equations are normalized (thus the degradation term set to 1), as well as the parameters :

• As introduced before, the goal of this model was to give us useful bases on which to work on. Then, we shall use the values of the parameters presented below as a "starting point". We shall present a double approach, composed of a theoretical and a simulation approach. Both approaches should interact so as to help us understand the way our system behaves.
• The obvious though process we propose consists in observing what happens with the simulation, then understand the source of these phenomenas. Finally, the ultimate goal consists in finding how we can pull the strings, hidden in the system, that control the behavior of the system.

Observations

---> petites oscillations + vérifier par le calcul ---> trop grande réactivité de flhDC

• First of all, let us see what the simulation gives, and what pieces of information we can get from it.
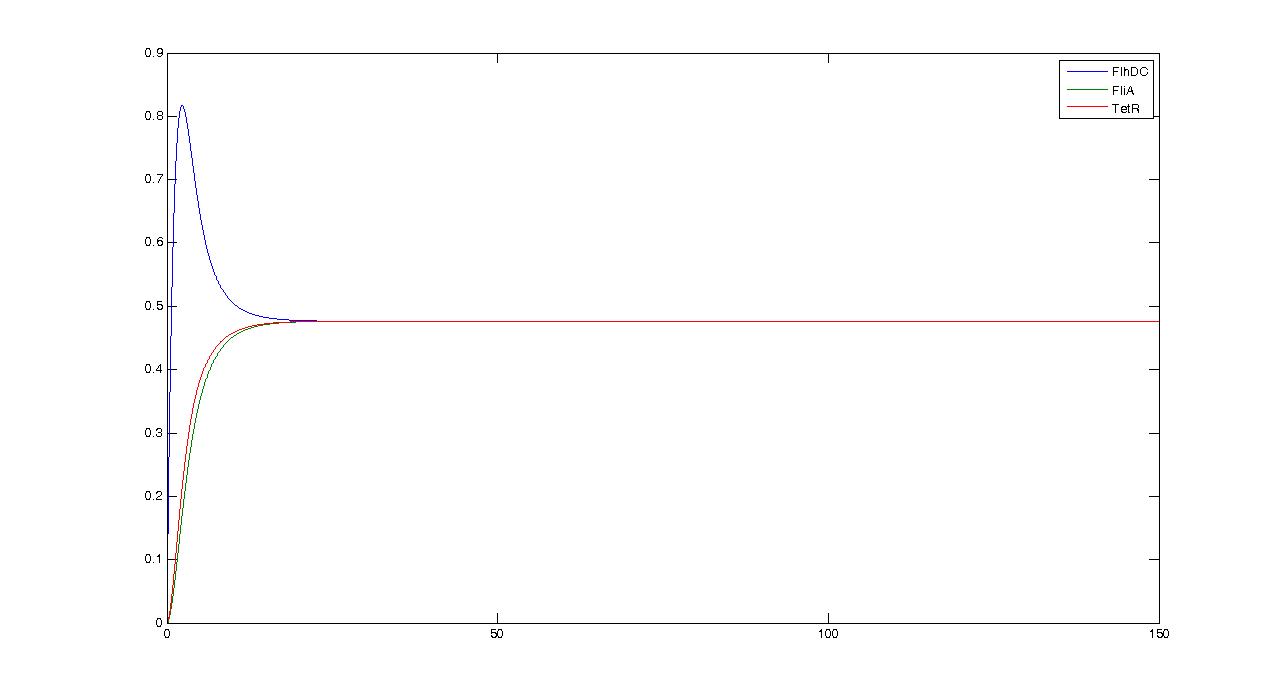
• Observation#1 :
  • By looking at this simulation, we could think that it is going to be hard to get oscillations...
    
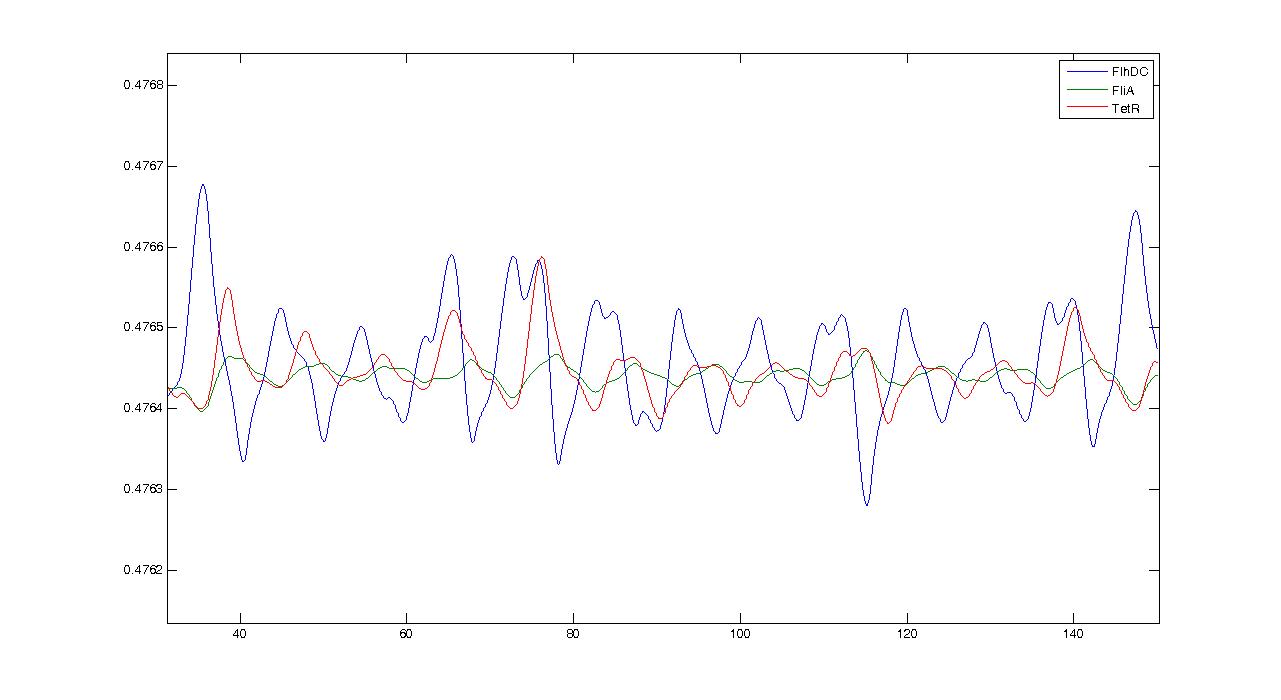
  • However when we zoom, we get this more reassuring view :
    
  • Conclusion : some intrinsic oscillations actually occur, but they seem to be strongly attenuated. The mathematical study shall help us decide whether these are only artefact oscillations. For example we shall try to check if the period observed (~10 time units) can be linked to mathematical data.
• Observation#2 :
  • Here, we need to change parameters a little bit, so that it becomes more obvious

Understanding the dynamics

• The classical approach consists in finding the equilibrium state, by setting

Then, we evaluate the jacobian matrix, so as to put the system under its linearized form:

which gives :

Then, we want to find the eigenvalues of the jacobian matrix, because they make us understand the behavior of the system. Here is the theoretical explanation :

The λ and γ coefficient make the convergence. In our case they are negative terms, which explains the fact that we have a quick convergence for the system. Ideally, it could be convenient to find which parameter influence this coefficient, so as to play with it and be able to propose a better control of the convergence.
The μ coefficient is responsible for the oscillations. In fact, in another base, with only real matrix, this would beget cosinuses and sinuses terms. Furthermore, it is strongly linked to the period of the oscillations.

We obtained three solutions :

We are only interested in positive real solutions. We can note that 0.4764 corresponds well to the experimental equilibrium value. Then we evaluated the eigenvalues for the jacobian :

Using these elements to improve the system and give directions to the wet-lab

dire qu'on peut tester les solutions pour obtenir une partie réelle aussi faible que possible, et qu'on peut jouer sur la période au moins

dire que pb c'es que mm en dim3, ca devient cho de gérer,mm si c la dim minimale

Entire System

//biocham ici//+ comparaison avec le modele hillistique

FIFO

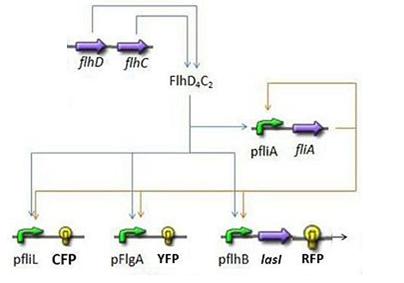
• The goal here is to present the results of the simulations we made concerning the FIFO part of the system.

Here is the system we implementated using Matlab (see the corresponding codes)

and the corresponding equations (for more detailed information see our establishment of the model).

where CFP, YFP, and RFP will be denoted below as respectively Z1,Z2 and Z3.

• We wanted to see if our predictions were accurate or not. We then solved the equations, forcing the behavior of FhlDC. In a first step, we imposed a constant production term of 1. Then, at a certain time, we set this production term to zero :

In fact we assumed that this behavior for FlhDC was acceptable regarding its estimated behavior in the whole system.

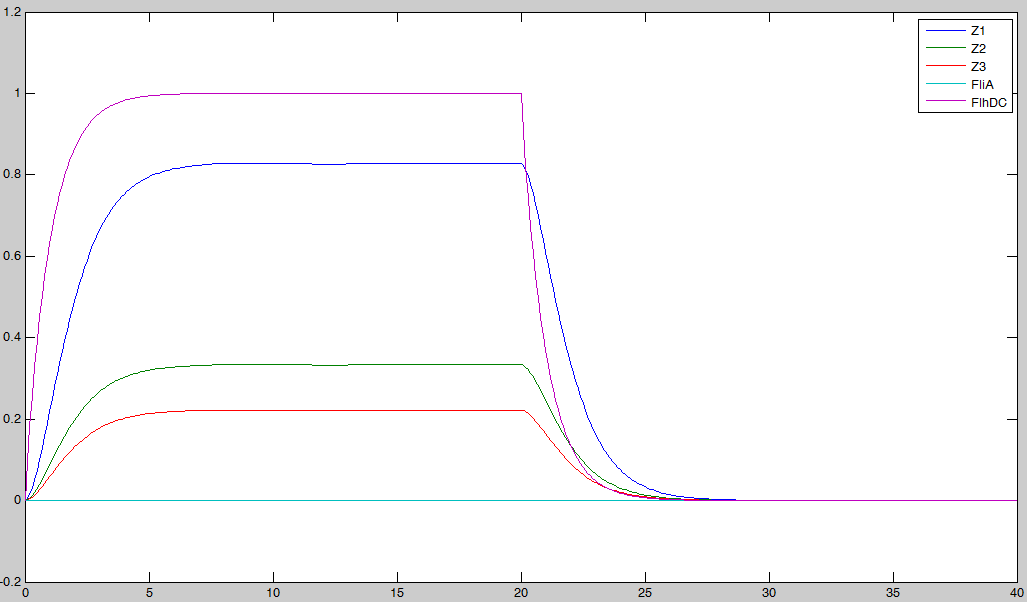
• We saw previously that without FliA, the FIFO would presumably not work. We then simulated a first system, where [FliA] stays to zero value.
  

We may see that there is a LIFO behavior rather than the FIFO we expect...

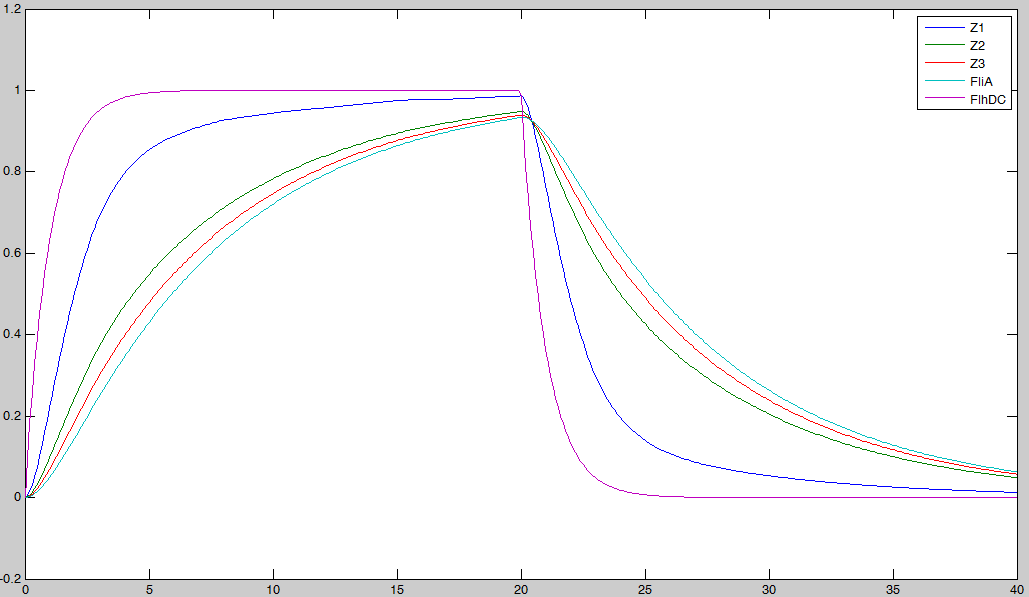
• Then, we simulated the entire system, to check if we had
  • the lasting burst due to FliA (more important for Z3 than for Z2, and more important for Z2 than Z1) in the increasing phase.
  • the effect of fliA which maintained the concentrations to their maximum (more important for Z3 than for Z2, and more important for Z2 than Z1) in the decreasing phase.
    

• We observe on these plots that the behavior is quite the one we expected, and that the FIFO is realized. FliA enables the curves to cross, and adds a delay on the genes that are most affected, with gives a better observability of the FIFO behavior.

Synchronization

Mathematical Analysis

Simulations and verification of the hypothesis