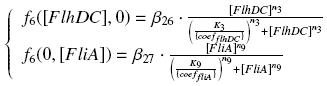Team:Paris/Modeling/f6
From 2008.igem.org
We have [FlhDC] = {coefflhDC}expr(pTet) = {coefflhDC} ƒ1([aTc]i)
and [FliA] = {coefFliA}expr(pBad) = {coefFliA} ƒ2([arab]i)
So, at steady-states,
| param | signification | unit | value | comments |
| [expr(pFlhDC)] | expression rate of pFlhDC with RBS E0032 | nM.min-1 | need for 20 mesures with well choosen values of [aTc]i and for 20 mesures with well choosen values of [arab]i and 5x5 measures for the relation below? | |
| γGFP | dilution-degradation rate of GFP(mut3b) | min-1 | 0.0198 | |
| [GFP] | GFP concentration at steady-state | nM | need for 20 + 20 measures and 5x5 measures for the relation below? | |
| (fluorescence) | value of the observed fluorescence | au | need for 20 + 20 measures and 5x5 measures for the relation below? | |
| conversion | conversion ratio between fluorescence and concentration | nM.au-1 | (1/79.429) |
| param | signification corresponding parameters in the equations | unit | value | comments |
| β54 | production rate of FlhDC-pFlgA with RBS E0032 β54 | nM.min-1 | ||
| (K48/{coeffliA}) | activation constant of FlhDC-pFlgA K48 | nM | ||
| n48 | complexation order of FlhDC-pFlgA n48 | no dimension | ||
| β55 | production rate of FliA-pFlgA with RBS E0032 β55 | nM.min-1 | ||
| (K49/{coefomp}) | activation constant of FliA-pFlgA K49 | nM | ||
| n49 | complexation order of FliA-pFlgA n49 | no dimension |
Then, if we have time, we want to verify the expected relation
 "
"