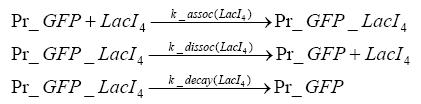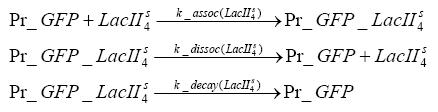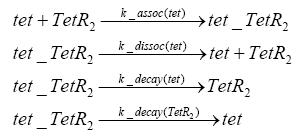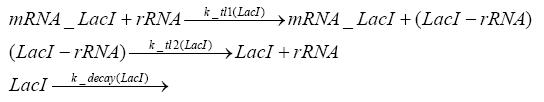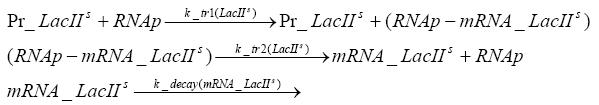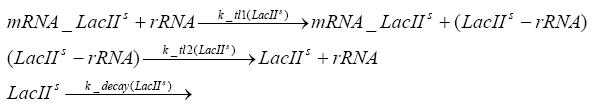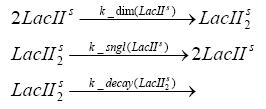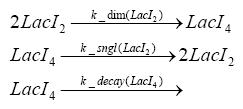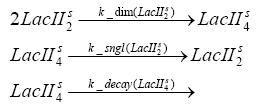Team:ETH Zurich/Modeling/Switch Circuit

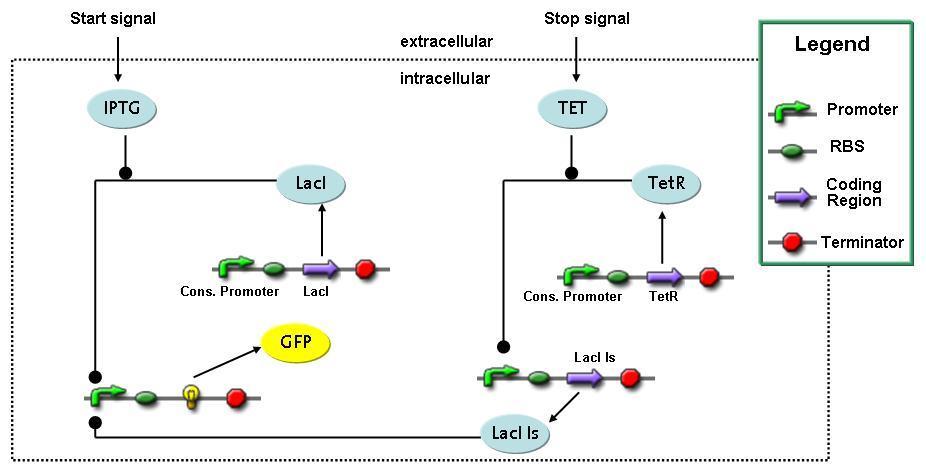
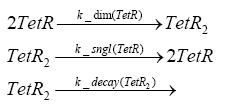
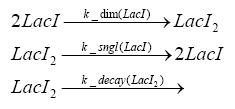
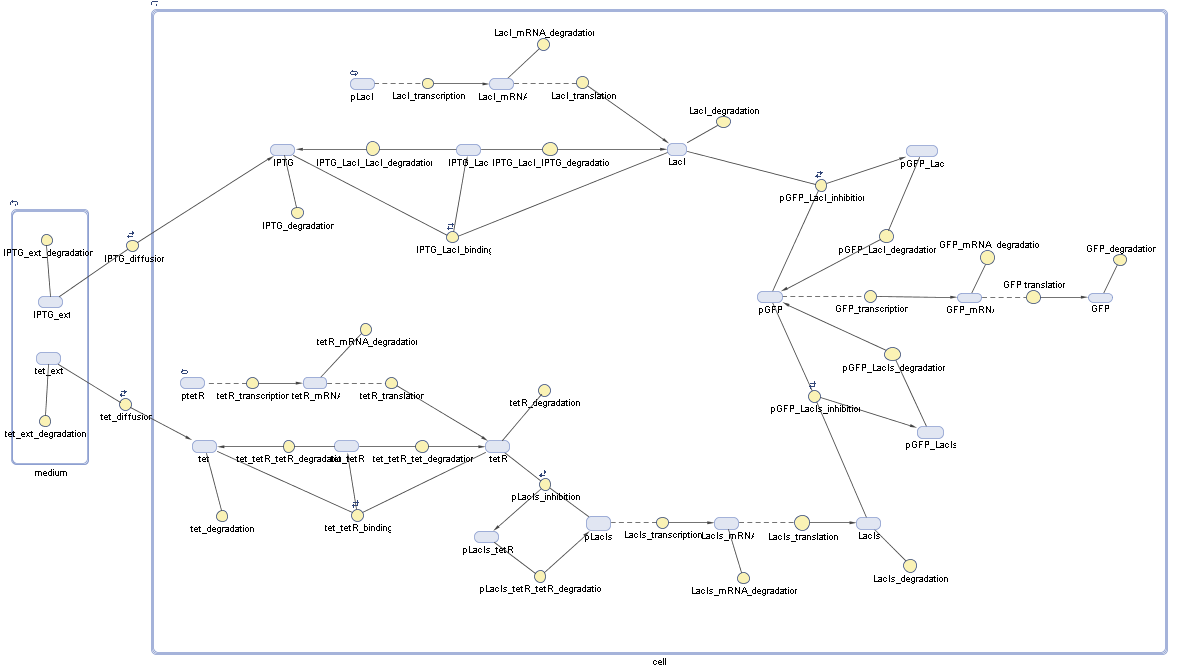
Switch Circuit

Detailed Model

diffusion of IPTG

In order to switch on the sircuit, we induce with IPTG. When we add the IPTG into the medium diffuses reversibly between the medium and the cells, where it is slowly degraded. In a chemostat extracellular IPTG is washed away.

diffusion of tet

The second inducer which is used in our system is tet. This also diffuses into the cell when it is added into the medium and degrades slowly.

binding of tetR to LacI-promotor and LacIIs-promotor

binding of LacI and LacIIs to GFP-promotor

binding of tet to tetR

binding of IPTG to LacI

transcription and translation of LacI

transcription and translation of LacIIs

transcription and translation of tetR

transcription and translation of GFP

dimerization of tetR

dimerization and tetramerization of LacI and LacIIs

Implementation and Simulation

For the sake of simplicity and because they wouldn't yield any significant effects on the results we are interested in, we neglected in all the transcriptions the additional step involving the RNA-Polymerase and in all the translations the step involving the ribosomes. Furthermore the effects of dimerization of tetR and the dimerization and tetramerization of LacI and LacIIs have also not been considered in the final impelemtation.

This simplified model still consisted more than 20 different species and over 30 kinetic reactions and has been implemented using the Simbiology Toolbox in MATLAB.

diagram view of the model

To get any useful results form the model, we performed deterministic and stochastic simulations based on Mass-Action-Kinetics. The stochastic simulations turned out to be computationally very exhaustive but generated no further significant information compared to the deterministic simulations.

Results and Discussion

The simulations show that our system actually should create a nice pulse-shaped expression of GFP. This expression can be started by inducing with IPTG and and stopped by subsequent addition of tet into the medium. By tagging the proetin, it degrades very fast so that the overall concentration is bounded and after activating the stop-signal, the remaining proteins disappear quickly.

Another fact, our simulations showed, is that in order to get one single pulse the tet-concentration inside the medium must not reach zero before all the IPTG has degraded too. Otherwise there would still be IPTG in the system inhibiting the binding of LacI to the GFP-prmotor and leading to an unwanted expression of our protein of interest as the LacIIs degrades.
One way to overcome this problem is by simply inducing with a much higher quantity of tet than IPTG, so that it simply takes longer for it to completely degrade or being washed away. Another way would be to wait a bit longer after the induction with IPTG so that it has already partly vanished until stopping the GFP-expression with tet.

Parameters

In this section you can find all the parameters used in the simulation.

References

(1) "Spatiotemporal control of gene expression with pulse-generating networks", Basu et al., PNAS, 2004

(2) "Genetic circuit building blocks for cellular computation, communications, and signal processing", Weiss et al., Natural Computing, 2003

(3) "Predicting stochastic gene expression dynamics in single cells", Mettetal et al., PNAS, 2006

(4) "Engineered gene circuits", Hasty et al., Nature, 2002