|
A simple mechanical model was developed by taking an analogy of B. subtilis propelled by its flagellum with that of a boat propelled by its motor. As the bacteria swims in the medium, it experiences two opposing forces: the flagellum force which propels it forward and drag force provided by the viscosity of the liquid medium. The drag force is analagous to friction which opposes the forward motion of objects on solid surfaces. The mechnical model is illustrated below:
From the figure above, we equate the drag force and flagellum force to obtain:
Solving this first order ODE, we derive an expression for cell velocity:
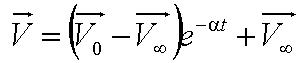 , where , where 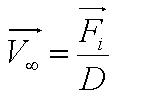
Solving the first order ODE for displacement, we derive an expression for cell trajectory:
Using our fitted data, we are able to determine parameters:
- Parameter A is the ratio of flagellum force to medium viscosity. It also represents the velocity of the cell after a sufficiently long time has elapsed, given that the flagellum force remains constant throughout its run.
- Parameter B is the initial cell velocity
- Parameter alpha is the ratio of the viscosity to the cell's mass.
In this model, we attempt to obtain a distribution for the flagellar force, which is represented by parameter A. We assume that the medium is homogenous and the viscosity is constant throughout the medium, hence the distribution of flagellar force will be sufficiently be described by parameter A.
|