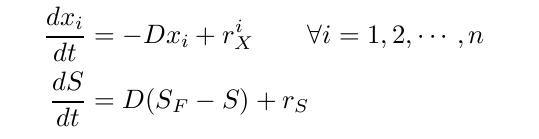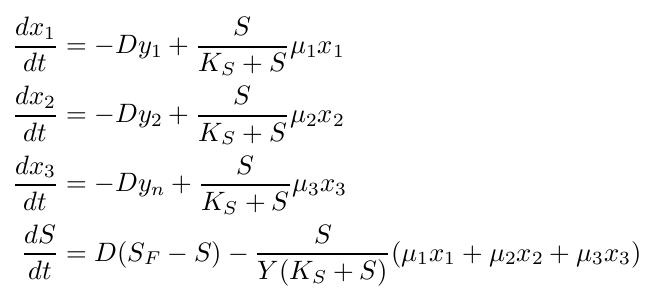Team:ETH Zurich/Modeling/Chemostat Selection

Chemostat Selection

As mentioned in the Project Overview page, one of the main concepts in our project is the possibility to select for organisms with reduced genome size. To achieve this we have thought of letting our system develop in a continuous environment with nucleotide limitation and base the selection method on the difference in growth rate. The aim of this model is to show the applicability of this concept and to determine the parameters for the operation of the chemostat in the lab.

The questions we are trying to adress with this model are:

• What are the ideal settings of nutrient concentration in the feed and dilution rate in order to select for reduced strains?
• What is the sensitivity regarding growth rate selection?
• What are the optimal timing parameters in order to induce two subsequent rounds of restriction enzyme gene expression?

We obtain the results for the calculated growth rates from the flux balance analysis performed in section Genome-Scale Model for the random deletions. These simulations performed in chemostat on the different strains are used to simulate the development of the population concentrations in continuous culture. The goal is to build a model in which we can vary parameters like substrate feed concentration and dilution rate to optimize the operation of the continuous culture in the lab as described in Chemostat Selection.

In the following sections we give a short introduction to continuous cultures and proceed to develop the used model.

Cemostat basics

A chemostat allows for continuous fermentation in a constant volume. It consists of a culture vessel with an input aperture for sterile medium and an overflow aperture to mantain the volume constant. This allows to mantain a constant population in the chemostat but still have continuous cell division.

Figure 1: Schematic of a chemostat

Here X is the concentration of biomass in kg/m3, S0 the feed concentration in kg/m3 and F Feed in m3/h.

By varying parameters like the dilution rate (D) and the concentration of nutrients in the medium, different steady states can be obtained, thus allowing to fine tune the selection process. In our case, the feed rate can be set externally and cell growth is limited by a selected nutrient (in our case nucleotides).

The specific growth rate in the chemostat can be determined by the material mass balances of biomass and substrate.

(Rate of accumulation)=(Input rate) - (Output rate) + (Production rate)

The equation for biomass and substrate are given by

Competition in the chemostat

We have extended the basic chemostat model to allow for selection of strains with reduced genome sizes by including mass balances for the biomass of more than one strain. We couple the differential equations in order to let the strains compete for the available limiting substrate. By changing parameters like dilution rate we can variate optimize the selection mechanism. We are interested in the effects of differences in growth rate and dilution rates on the sensitivity of our method to validate our assumptions.

Figure 2: Three different strains competing in a chemostat

In this figure we observe three different strains competing in the chemostat.

• In the first case, Strain 1 has the highest growth rate and as expected after some time reaches the highest biomass in the reactor, although the initial concentration is the smallest.
• Strain 2 has a higher biomass concentration at the beginning, but due to the slightly smaller growth rate is eventually outgrown by strain 1.
• Strain 3 has a growth rate that is smaller than the dilution rate and thus is washed out irrespective of the initial concentration.

The simulation results confirm our assumptions that a selection for strains showing different growth rates is possible under adequate conditions.

To estimate the the parameters needed to further develop our model we used the model for flux balance analysis, as presented in section Genome-Scale Model. In our model the uptake rate of thymidine is 0.016 mmol/h (this is equivalent to 0.0038 g/h). With this parameter we calculate the yield for our initial population:

The yield can be directly computed with this model, as the growth rate and the thymidine uptake rate can be directly used to calculate these parameters.

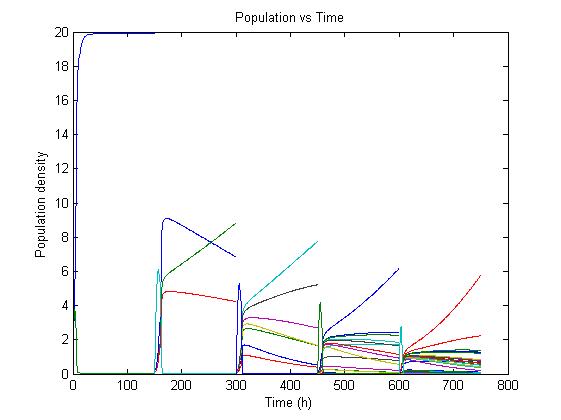
The simulation files can be found here.

Pulse

The next step in our model is to simulate the effect of pulsing the expression of restriction enzyme in our populations. We start the culture with a wild type strain and let it grow to steady state. By applying a pulse as described in the Genome Reduction section we generate mutants. For this model we have assumed that the expression of restriction enzymes will be very aggressive, killing almost everything in the culture vessel and generating a small amount of mutants with reduced genomes (this assumption can be easily changed in our model). As this step is used to estimate the sensitivity of the selection mechanism, we have varied the growth rate of the mutants by a random change in growth rate of 0.03.

This allows to estimate the settings for dilution rate and substrate feed concentration as the difference in growth rate, as this difference in growth rate corresponds with the sensitivity described in the literature [1].

In the next section we will present the results with data obtained from the Genome-Scale Model.

Figure 3: Selection of strains after multiple pulses

The preceding figure shows the possibility to select for strains after a variable number of reduction rounds. We observe, that with increasing number of deletion rounds the sensitivity of the selection method is the limiting factor. Small differences in growth lead to an increase in necessary time to separate the different strains. In this first estimate, the model shows that the strategy to be followed is an increase of selection time between pulses. This is accounted for in the framework where we include the computed growth rates for the reduced mutants.

The differential equation for these three strains are described as follows

The simulation files can be found here.

Results

In Figure 4, you see the Simulation of Chemostat which was modeled as follows:

where the parameters are ....

(K_s = 0.08, Sf = 10, D = 0.55, Y = 2, S0 =8) This simulation results were obtained using restriction enzyme SmiI. Every 100h a pulse of this restriction enzyme was given to the current population. The growth rates of mutants vary between 0.6114 and 0.6174.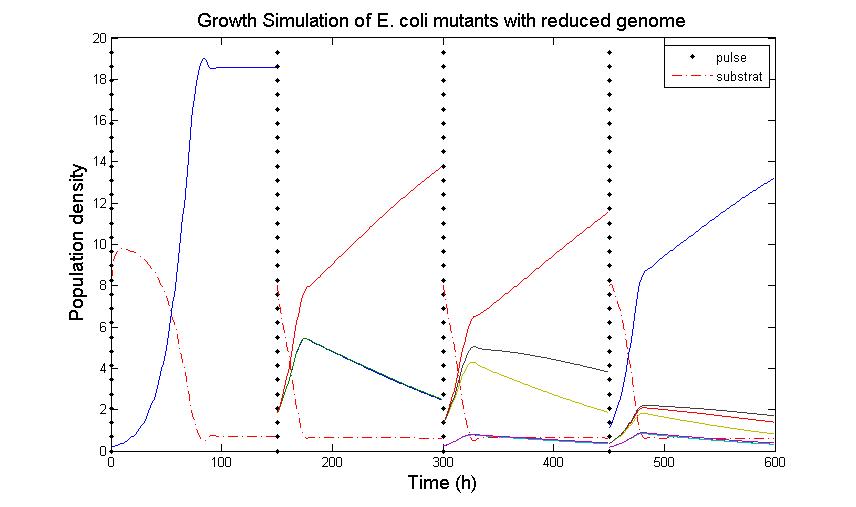

Figure 4: Growth Simulations of reduced-genome mutants. The black points denote a pulse of restriction enzyme which was given every 100 h. Dashed red line denotes the concentration of substrat, namely amount of Thymidin. The uptake rate of thymidin was set to 0.016 1/h. The other curvea describe the growth of reduce-genome mutants. In our model, each pulse of restriction enzyme reduces the current population dramatically and leads to emergence of mutants. The simulation assumes that from each strain maximally two mutants can be generated and their conentration is proportinal to the amount of this strain before pulsing with restriction enzymes. During the whole simulation(4 pulses with duration of 100 h) the whole population is assumed to be present in the chemostat.

We have shown that a selection mechanism based on growthrate, as predicted by the Genome-Scale Model, is theoretically prossible.

We have further estimated a first feasable range for the principal parameters, including dilution rate and feed concentration. In our case and for a difference in growth rate of 0.03 we find values of D= and Sf=

We further have a first estimation of the regeneration time between pulses. Here we have also a first set of parameters for the time between pulses of 150 hours, with regeneration times twice as high every 5 to 8 pulses.

References

(1) "Selection in chemostats." ,D E Dykhuizen and D L Hartl, Journal of Bacteriology, Microbiol Rev. 1983 June; 47(2): 150–168.
(2) "Biological Reaction Engineering Dynamic Modelling Fundamentals with Simulation Examples", Dunn, Irving J. / Heinzle, Elmar / Ingham, John / Prenosil, Jiri E., Wiley-VCH Verlag GmbH,. Weinheim, 2003