|
The following mechanical model was developed.
From the figure above, we equate the drag force and flagellum force to obtain:
Solving this first order ODE, we derive an expression for cell velocity:
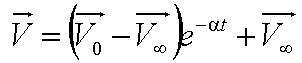 , where , where 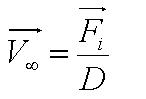
Solving the first order ODE for displacement, we derive an expression for cell trajectory:
Using our fitted data, we are able to determine parameters:
In this model, we attempt to obtain a distribution for the flagellar force, which is represented by parameter A. We assume that the medium is homogenous and the drag coefficient is constant throughout the medium, hence the distribution of flagellar force will be sufficiently be described by parameter A.
|