Team:ETH Zurich/Modeling/Genome-Scale Model

Genome Scale Analysis

In the Restriction Enzymes Analysis modeling section we deal with the analysis of restriction enzymes effects on the genome from the simple point of view of nucleotide sequences and cutting patterns. This is not informative enough when we try to understand if the key principles of reduction and selection at the base of our minimal genome approach are valid in the context of the whole cell response. It is evident that our selection method for smaller genome size strains is based on the assumption that is possible to control growth rate as a function of its genome size. As explained in the Project Overview, we put a selective pressure on the genome size by combining two effects together: the random reduction of the genome size by restriction enzymes cutting and the feeding of a limited amount of thymidine nucleotides on the background of a thymidine auxotrophic strain. In this context, one should also consider the effects that the lost of chromosomal coding regions may have on the physiology of the cell. This scenario needs to be validate using modeling techniques that relate genome content and substrates avaiability with cell physiology, on a system level fashion. Fortunately, in the last ten year huge progress have been achieved in coding our understanding of biological networks into whole cell comprehensive stochiometric models. This model typology is called genome scale modeling and we use the most update genome scale model for our working strain (E.Coli K12 MG1655) in order to answer the following questions:

• Is it possible to slow the growth of a strain by using a thymidine auxotrophyc strain and limiting thymidine feeding? How are thymidine uptake rates (concentration in the medium) quantitatively related to the growth rate in the auxotrophyc strain background?
• What is the quantitative effect on growth rate when reducing the genome size of wild type strain (under the assumption of not losing any functionality)?
• What is the combined effect of thymidine limitation and genome reduction on growth rate? It is possible to identify the best initial and running settings?
• What are the best restriction enzymes to be used in order to maximize genome reduction and at the same time vitality (growth rate) of thymidine auxotrophyc strains?
• What is the predicted genome reduction difference if the cell are grown in minimal or very rich medium (in term of nutrients)?
• What are the differencies if we were to use alternative approaches to our reduction and selection methods such as complete random search or methodical knockout strategy?

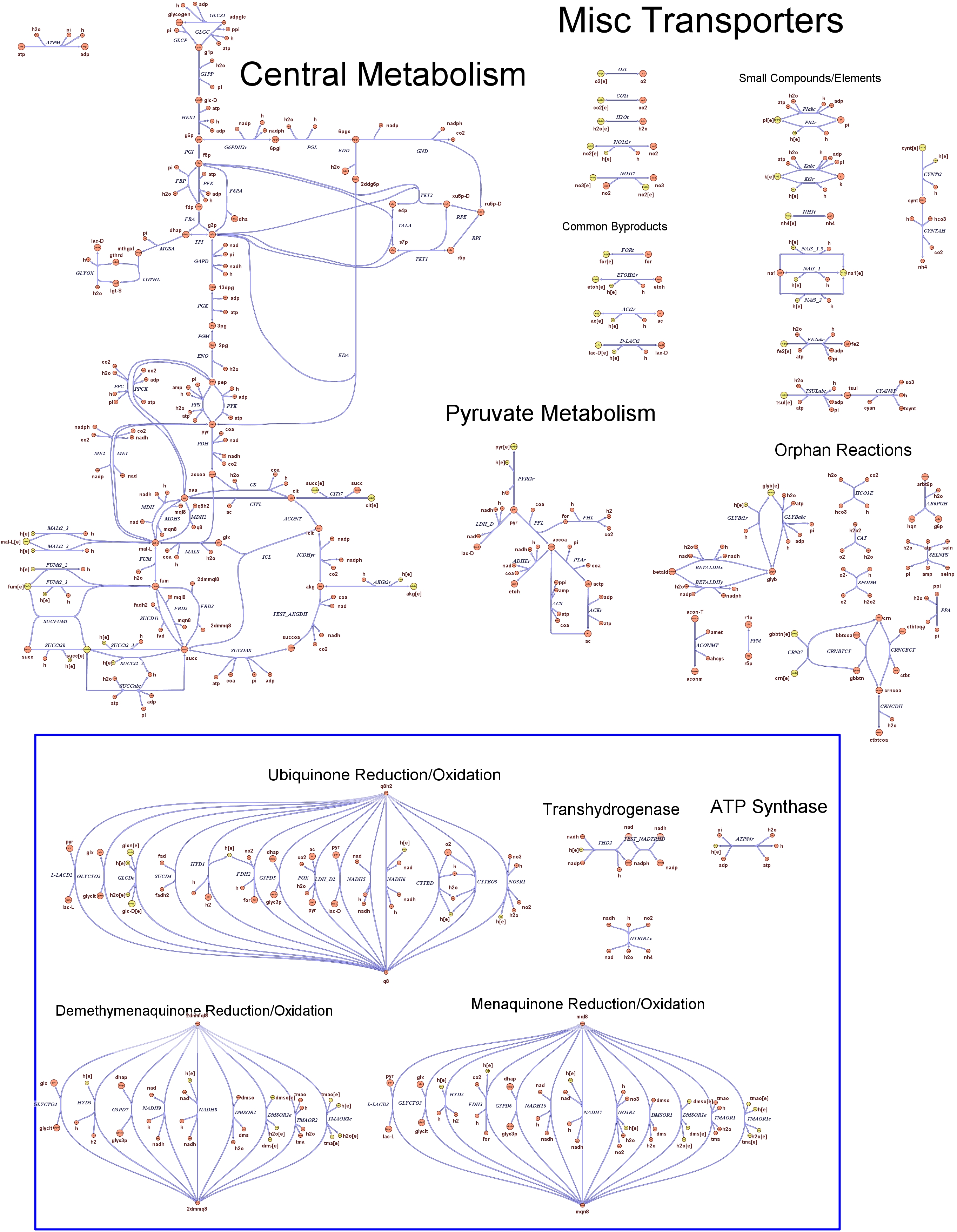
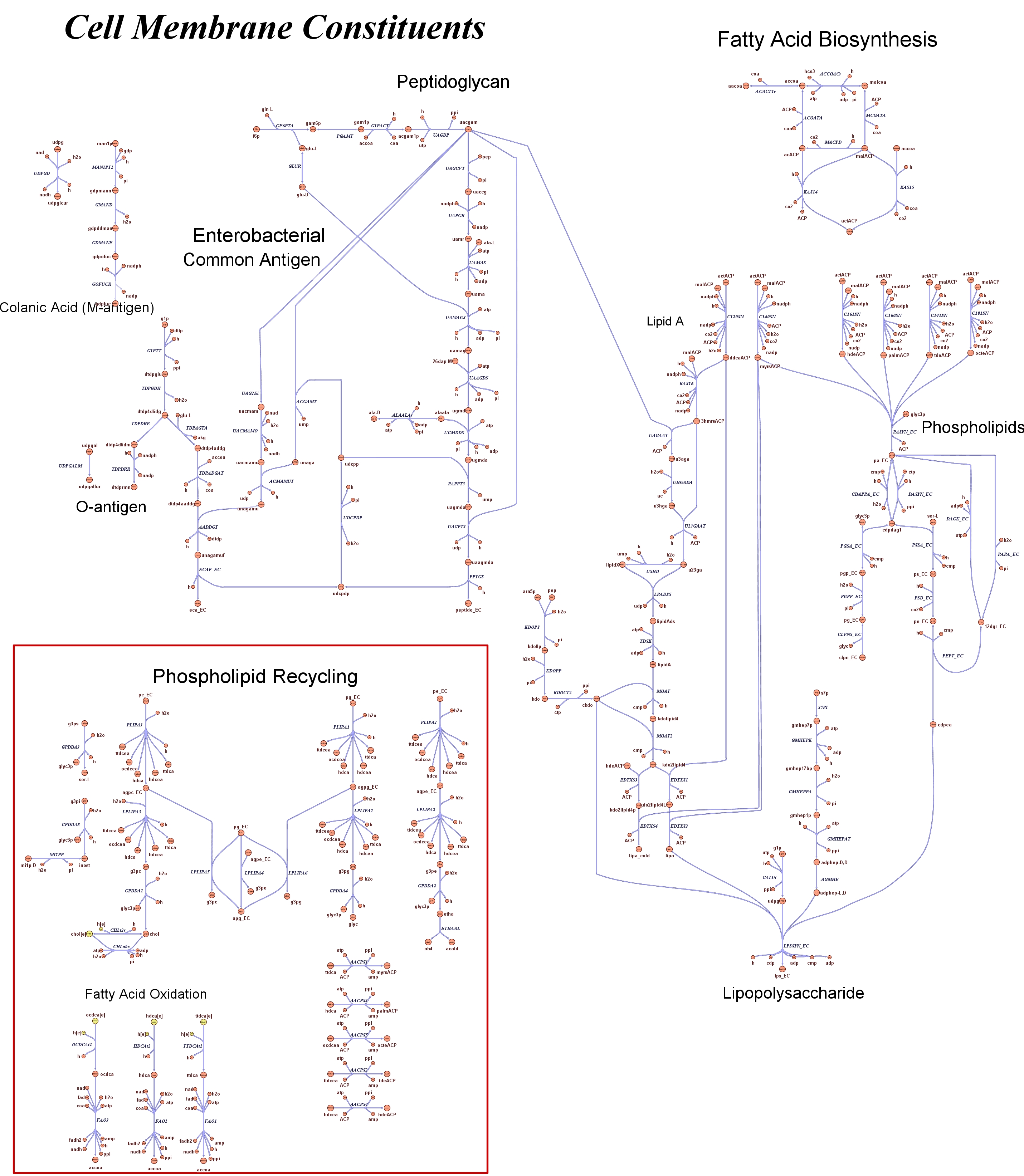
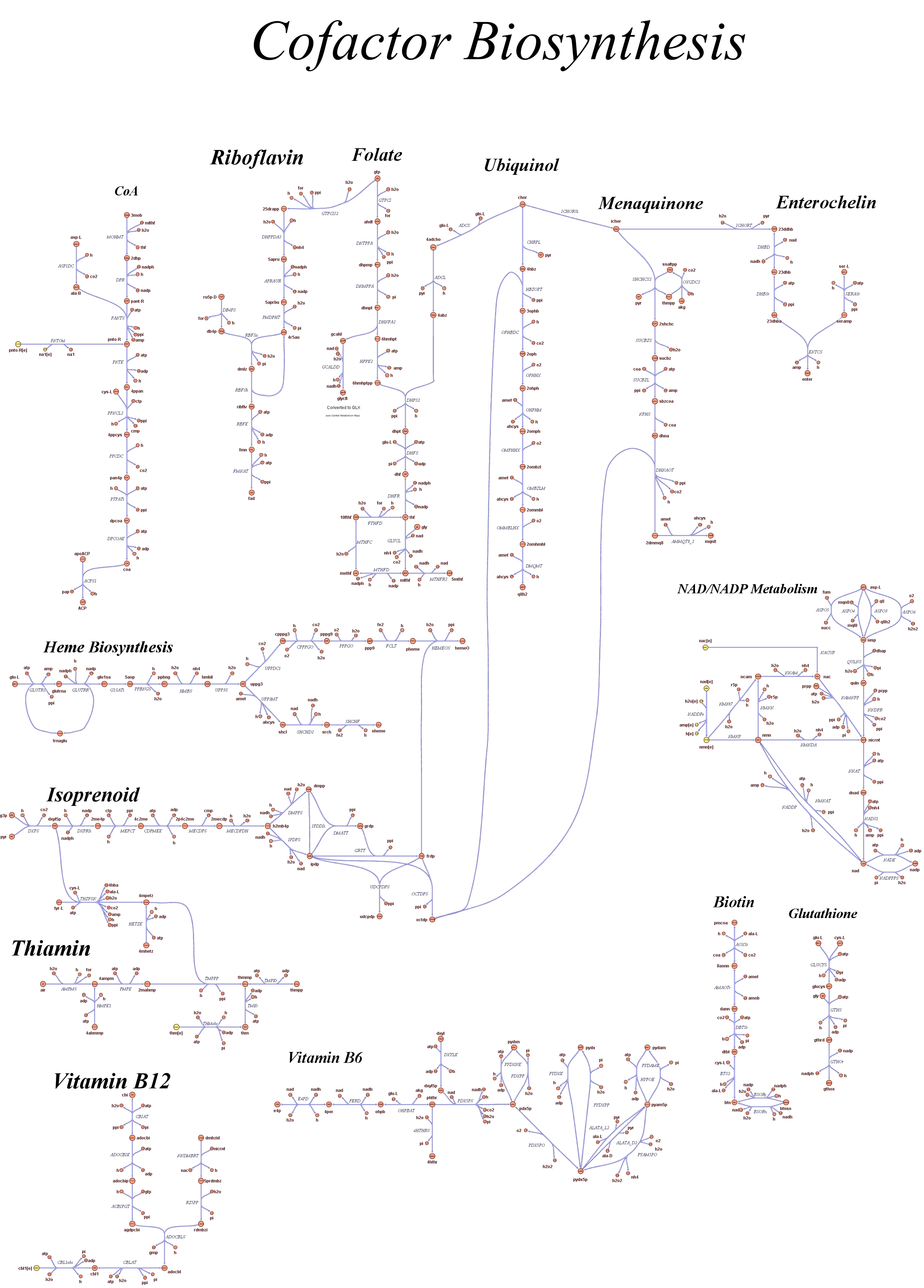
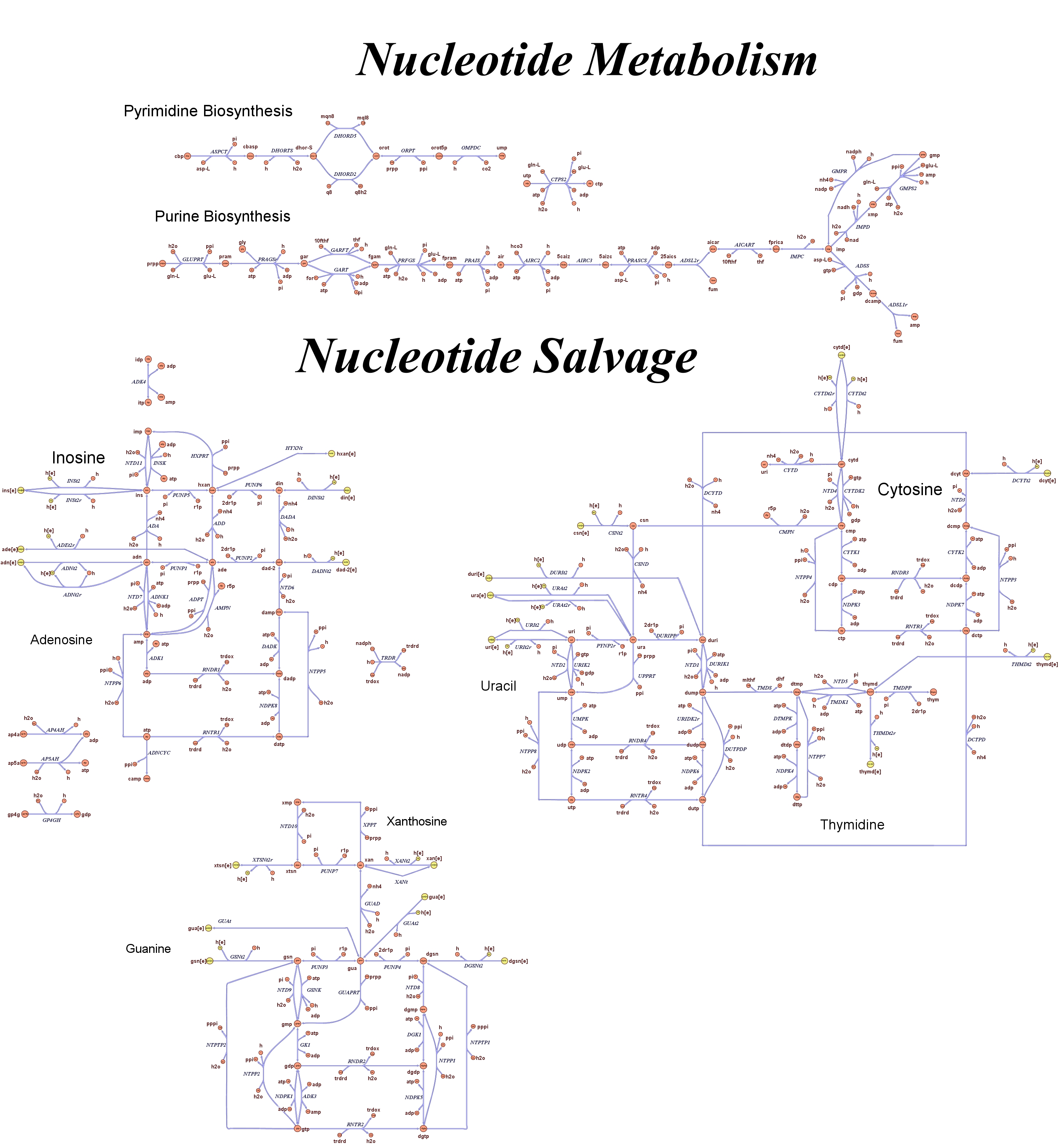
These questions are answered below, in the respective sections. As first we introduce the genome scale model concepts, the Flux Balance Analysis theory and in particular the iAF1260 E.Coli Genome Scale Model developed by [http://gcrg.ucsd.edu/|the Palsson's Group at UCSD], that we modified and used. In the following sections we show the results of simulations for the different questions to be answered.

Genome Scale Models, FBA and E.Coli K12 MG1655

Genome scale models are biological network reconstructions that effectively mape genome annotations (ORFs) to biochemical reactions that define the metabolic network specific to a particular organism. They are also called stoichiometric models because encode calculation of quantitative relationships of the reactants and products in the balanced biochemical reactions in the organism. When they are enough informative to cover a consistent part of the known organism functions are called in-silico organisms, bacause it is possible to use them as models to simulate whole cell system responses. Genome scale models are used in combination with Flux Balance Analysis in order to predict the physiology (growth rate, uptake rates, yields etc..) of the in-silico organism depending on variable external nutrient conditions or changes in genome composition (in-silico knockout experiments). In the last decade this modelling technique has proved to give consistent results with experimental data under various hetereogeneous conditions of testing (4). Mathematically, Flux Balance Analysis uses the stoichiometric information in order to predict the metabolic flux distribution under the assumption of maximization of a particular cell process (for example maximizing biomass production). If N is the stochiometric matrix, and V the vector of fluxes, Flux Balance Analysis assumes steady state:

And then compute a flux solution according to a maximization (or the correspective minimization) function:

Once the metabolic fluxes are known, is possible to calculate physiology parameters. For a complete introduction to these concepts please read this [http://www.nature.com/nbt/web_extras/supp_info/nbt0201_125/info_frame.html| Genome Scale Models introduction].

Focusing on the organism of our interest, the E. coli in silico organims we use is iAF1260 and includes the genes involved in central metabolism, amino acid metabolism, nucleotide metabolism, fatty acid and lipid metabolism, carbohydrate assimilation, vitamin and cofactor biosynthesis, energy and redox generation, and macromolecule production (i.e. peptidoglycan, glycogen, RNA, and DNA). In order to give a flavour about the pathways included in the model we post the graphical representation of reactions and metabolits that has been produced for the previous model version (4).

Central Metabolism

Amino Acid Metabolism

Cell Membrane

Cofactor Biosythesis

Nucleotide Metabolism

Alternative Carbon Sources

Thymidine limitation effects on growth rates

Genome size effects on growth rates

Different mediums

Growth rates as output of whole cell system behaviour

Comparing different approaches to minimal genome

References

(1) "Thirteen Years of Building Constraint-Based In Silico Models of Escherichia coli" ,Jennifer L. Reed and Bernhard Ø. Palsson, Journal of Bacteriology, May 2003, p. 2692-2699, Vol. 185, No. 9
(2) "A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information", A.M. Feist et al., Molecular Systems Biology 3:121
(3) "Quantitative prediction of cellular metabolism with constraint-based models: the COBRA Toolbox", S.A. Becker et al., Nature Protocols, 2007
(4) "In silico predictions of Escherichia coli metabolic capabilities are consistent with experimental data.", Edwards JS, Ibarra RU, Palsson BO (2001), Nat Biotechnol, 19: 125–130.