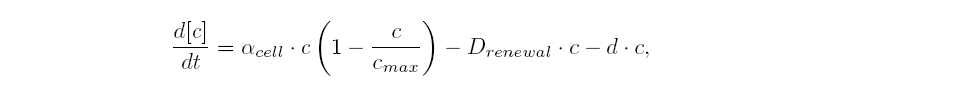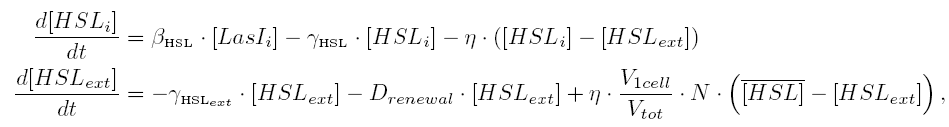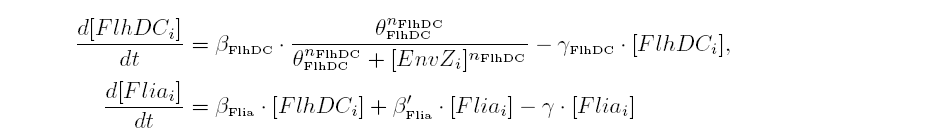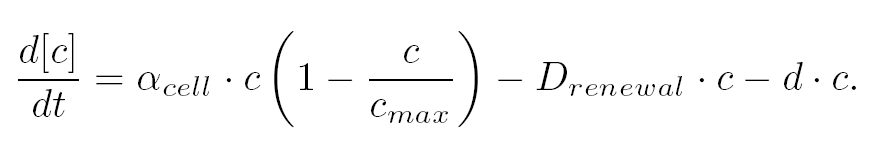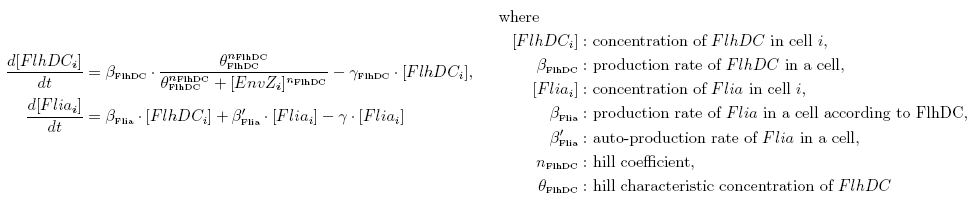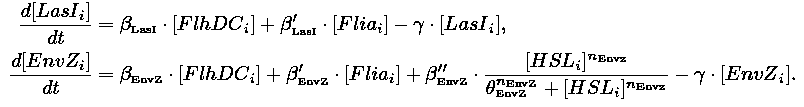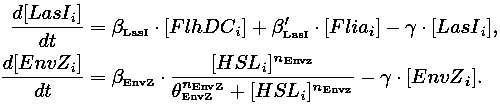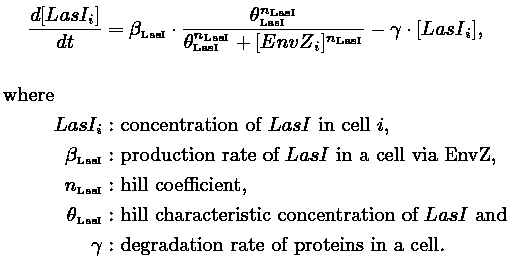|
Model Construction
Introduction
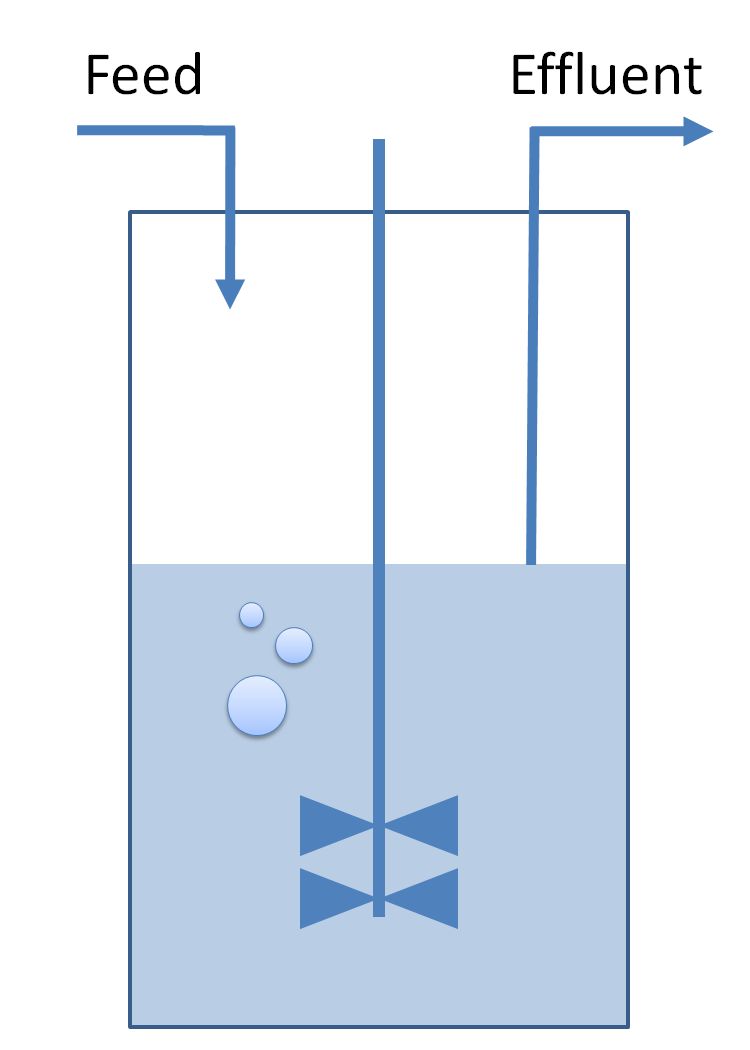
In this section, we investigate possible improvements of the core system. Our objective is twofold : the system has to provide sustained oscillations and these oscillations should be synchronized amongst a population of cells. To this aim we explore designs inspired by quorum sensing and model in a chemostat cell growth and species diffusion outside cells. We consider two models relaying on different designs principles.
↓ To joint our quest for alternatives click here! ↑
Modeling Alternatives
The proposed models are:
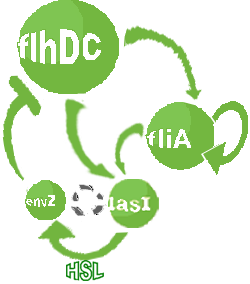
| Bimodular System
| Unimodular System
|
| 
|
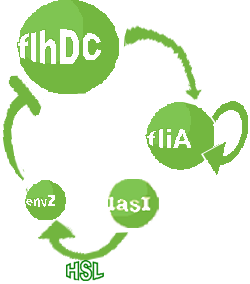
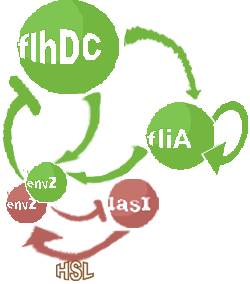
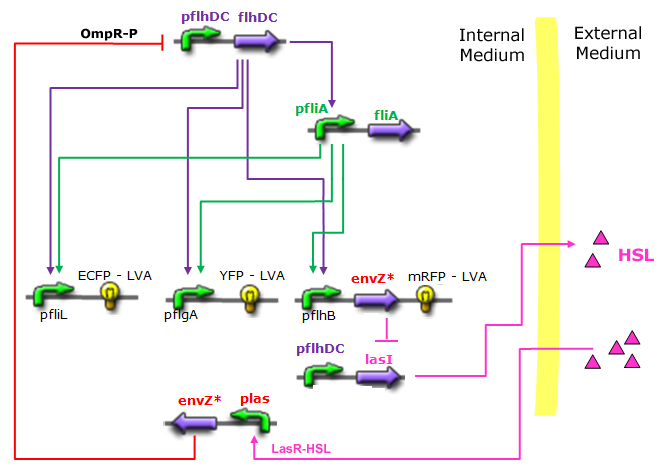
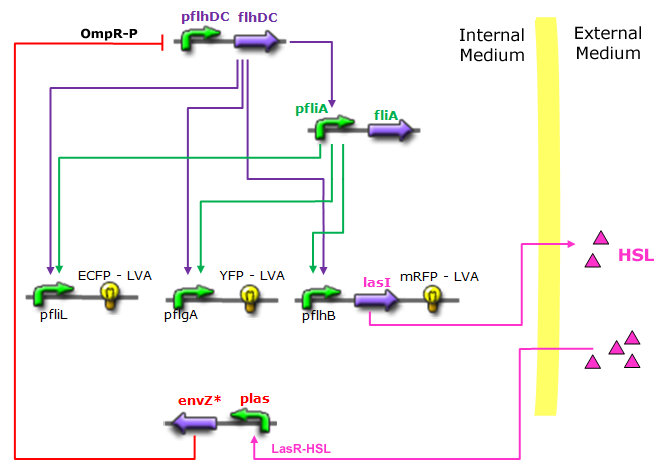
- In the first system, we use a modular design. We consider that the core system is one of the modules of the system and that the other module is a three gene oscillator system presented in [Garcia-Ojalvo] that accounts for quorum sensing. We call this alternative the 'bimodular system'.
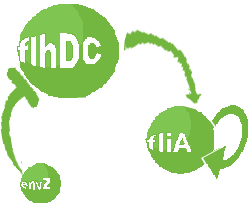
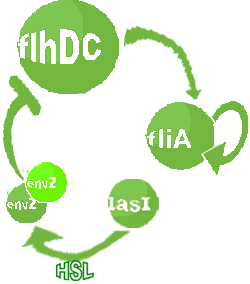
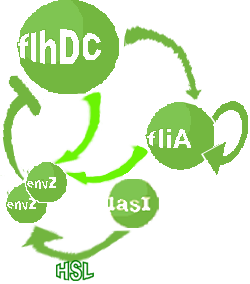
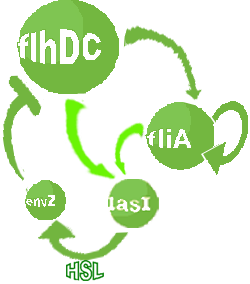
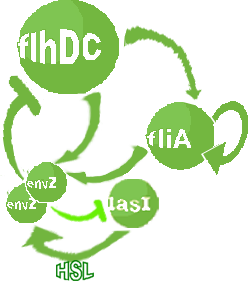
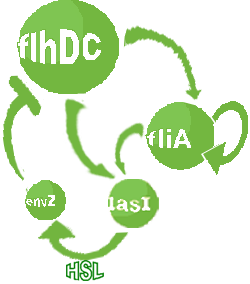
- In the second system, namely the 'unimodular system', we rewire the architecture of the core system to introduce delay via HSL export in the environment in a single circuit.
Both the bimodular and unimodular systems describe events that happen not only at the cellular level (as in the core system) but also at the population level due to interactions needed between a cell and its environment.
In the following sections, we first describe population modeling (the common part among our two proposed models) to then focus our attention to the characteristics that are exclusive to each of the modeling alternatives.
Common Description
| Use of chemostat:
|
|
|
| Use of quorum sensing:
|
|
|
| Use of some interactions from the core system:
|
|
|
↓ read more on common dynamics... ↑
| Common Dynamics: Chemostat
|
| The variation of cells' concentration in the chemostat over time can be expressed in terms of a production (positive) term and degradation (negative) terms:
|
|
|
| For the production term, we use a logistic equation to model cell growth, according to standard assumptions. The behaviour obtained is the following one: at low population density, the concentration of cells in the chemostat (c) increase exponentially with a growth rate αcell and at high population density, the population reaches a maximum concentration, cmax.
|
| For the degradation term, we consider that c decrease proportionally to both a dilution phenomena cause by the renewal of the medium in the chemostat (Drenewal) and cell death (d).
|
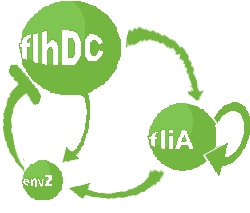
| Common Dynamics: Quorum Sensing
|
| In order to model the quorum sensing dynamics, we consider that:
|
| 1) Inside a cell, the HSL concentration increases proportionally to the concentration of LasI and decreases according to both a degradation term (proportional to the internal HSL concentration) and a transport term (proportional to the difference between the internal and external concentration of HSL). Thus, the equation for the internal HSL concentration is:
|
|
|
| 2) Outside the cells, HSL is accumulated with the same transport term that we use in the previous equation. The degradation of HSL in the external medium and the dilution controlled via the chemostat accounts for HSL external decrease. So the external HSL concentration is given by:
|
|
|
| that is equivalent to:
|
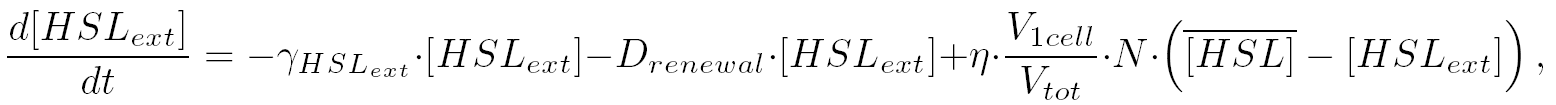
|
where 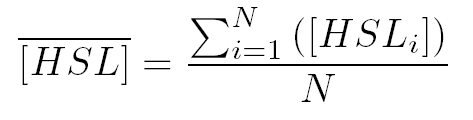 and and 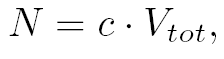
|
| Common Network Dynamics: FlhDC and Flia
|
| FlhDC and Flia are regulated in the same way in both systems. FlhDC is produced under the influence of EnvZ via an inhibition. Flia is regulated for its self and FlhDC.
|
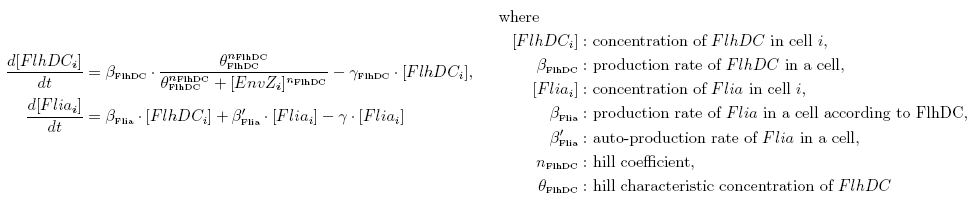
|
|
Alternatives Description
| Bimodular System
| Unimodular System
|
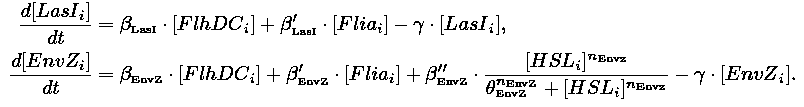
| 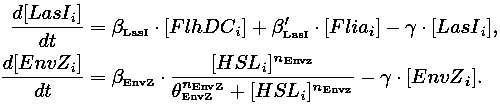
|
| Core system coupled with an oscillator
| Modified core system that accounts for quorum sensing
|
↓ read more on alternatives description... ↑
Kinetic parameter values
The following table sumarize our findings. Theses parameters values are used during the simulations. Most them are found in literature others are obtained from further analysis.
| Parameters
|
|
|
| Chemostat
| Parameter
| Meaning
| Original Value
| Normalized Value
| Unit
| Source
|
|
| αcell
| Growth rate
| 0.0198
| 1
| min-1
| wet-lab
|
| cmax
| Carrying capacity for cell growth
| 0.1
| 0.1
| µm3
| [3]
|
| Drenewal
| Dilution rate
| 0.00198
| 0.1
| min-1
| wet-lab ([3])
|
| d
| Death rate
| 0.0099
| 0.5
| min-1
| wet-lab
|
|
|
| Quorum Sensing
| Parameter
| Meaning
| Original Value
| Normalized Value
| Unit
| Source
|
|
| γHSL
| Degradation rate
| 0.0053
| 0.2690
| min-1
| wet-lab
|
γHSLext
| Degradation rate
| 0.0106
| 0.5380
| min-1
| [2]
|
| βHSL
| Production rate
| 0.3168
| 16
| min-1
| ∅
|
| η
| Diffusion rate
| 10
| 505
| min-1
| [2]
|
| nHSL
| Hill coefficient
|
| 4
|
| [3]
|
| θHSL
| Hill characteristic concentration for the second operator
|
| 0.5
| c.u
| [3]
|
|
 "
"