|
Our model is based on the crucial role played by nutrients, and other resources, during the main growth phases that B. subtilis undergoes - the lag phase, the exponential phase and the stationary phase. To keep the model simple, we omit the fourth phase of growth - the death phase.
Lag Phase
During the lag phase, the rate of growth is slow. All nutrients are situated outside the cell initially. Some time is needed for an adequate amount of nutrients to move from the outside of the cell into the interior of the cell. This is vital, as the cell requires the nutrients for growth.
Exponential Phase
Nutrients are consumed during cell growth and the growth is exponential as long as there are enough nutrients available. The exchange of nutrients ensures that the intra- and extracellular nutrient concentrations are the same.
Stationary Phase
The growth of the colony ceases in number and in volume. This happens when the colony has consumed all available nutrients. Other contributing factors may be death and cell division.
We chose to represent the growth in terms of overall volume rather than number of cells.
For small volumes (lag phase and early exponential phase) the volume is a smoother variable (the overall volume grows a little in the lag phase) while in later phases, the volume and the number of cells are proportional.
Considering the overall volume also regularises the process since it allows us, to some extent, to overlook the process of cell division during the bacteria growth. We can assume the internal concentration of nutrients is reset almost instantaneously to the external concentration. During this time, the total volume does not change.
In order to couple growth with resources, our model curbs the optimal growth rate of the volume (A) as a function f of the resources R. We used a Hill function of exponent n, as it models with only one parameter the fact that production is unhindered when resources are plentiful and minimal when resources have run out. Finally we assume that in term of resources the cost of an extra unit of volume is alpha.
The growth of the overall volume V is therefore modelled as:
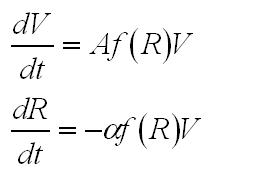
f(R) is the Hill function, where
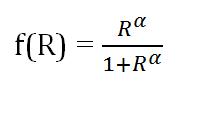
Its switch point is 1.
The M-file we wrote for the growth model can be found in the Appendices section of the Dry Lab hub.
|