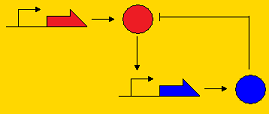
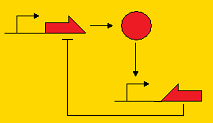
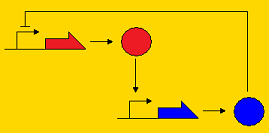
Sequestillator Modeling

The creation of a synthetic genetic clock has been considered by many people to be a "holy grail" of synthetic biology. Elowitz's "Repressilator" was one of the first synthetic clocks constructed, and it paved the way for consideration of other topologies that may promote oscillatory behavior, such as the Atkinson clock. A common characteristic of genetic clocks in general is the presence of a negative feedback loop (i.e. A activates B, and B represses A, so by repressing A, B indirectly its own concentration). In the Repressilator and the Atkinson clock, this repression occurred on the pre-transcriptional level; that is, the repressor protein prevented transcription of the activator gene. Below, we present three topologies of clocks with their modes of repression.

Note that the pre-transcriptional repression topology is the Atkinson clock without the positive feedback loop, and the post-translational clock is the Sequestillator. One of the goals of the modeling team is to understand the dynamics of this repression loop - i.e., how does the type of repression effect the robustness of the oscillator and the behavior (amplitude, periodicity, etc.).

Analytically, it's pretty tough to answer these questions due to the multiple nonlinearities associated with the ODEs. However, numeric techniques can prove useful in helping answer our questions about robustness and behavior. We can pick lots of different, physiologically relevant parameter sets, put them into our ODEs, and see what trajectories we get. Particularly, going back to our question about robustness, we can assign a value for robustness. We define this value as the total number of parameter sets that give oscillatory behavior over all possible feasible parameter sets. Within our lab, we call this value the Ninfa index.

Our general algorithm for "selecting" for oscillations is as follows:

• For a parameter set, use ODE Solver to get trajectories. Take one of those trajectories, select a time period that allows the dynamics to evolve appropriately (i.e. chose a time period that is several generations away from t=0) and do the following:
• Apply Fast Fourier Transform on trajectory to get a Power Spectral Density - there should be two symmetric peaks if there is a chance for oscillatory behavior. However, sometimes damped oscillations creep and the PSD shows two peaks.
• Low Pass filter: max sure the maximum Fourier coefficient is larger than a specific, relatively small value. This gets rid of really, really small oscillations that may be attributable to numeric errors, and wouldn't be detected experimentally anyways.
• Damping test

We created the "Indexilator" to calculate "relative" Ninfa indices (instead of dividing by the total feasible range of parameter space, divide by the number of trials you ran). The "Indexilator" is coded in Mathematica (we are currently working on programming a MatLab version).

Ninfa Index Calculator of Simple Model:

• Stochastic comparison of all three oscillators