|
A simple mechanical model was developed by taking an analogy of B. subtilis propelled by its flagellum with that of a boat propelled by its motor. As the bacteria swims in the medium, it experiences two opposing forces: the flagellar force which propels it forward and drag force provided by the viscosity of the liquid medium. The drag force is analagous to friction which opposes the forward motion of objects on solid surfaces. The mechanical model is illustrated below:
Mechanical Model of Motile B.subtilis
From the figure above, we equate the drag force and flagellar force to obtain:
Solving this first order ODE, we derive an expression for cell velocity:
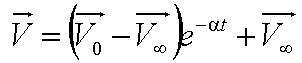 , where , where 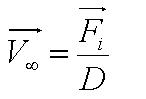
Solving the first order ODE for displacement, we derive an expression for cell trajectory:
Using our fitted data, we are able to determine parameters:
- Parameter A is the ratio of flagellar force to medium viscosity. It also represents the velocity of the cell after a sufficiently long time has elapsed, given that the flagellar force remains constant throughout its run.
- Parameter B is the initial cell velocity - in practice the velocity as we started to track the cell
- Parameter alpha is the ratio of the viscosity to the cell's mass.
As is widely known, the movement of bacteria is not that simple. Many bacteria have two distinct modes of movement: forward movement (swimming) and tumbling (1). Tumbling allows them to reorientate, thus making their movement a three-dimensional random walk.
Our mechanical model can be used to analyse the swimming movement of bacteria with a few extra assumptions:
- The medium is homogenous and its viscosity is constant throughout the medium.
- The swimming movement is made of a finite number of trajectories that can be modelled with our mechanical model. Such an assumption corresponds to the idea that the bacteria's flagellum propels it in a constant direction for a certain period of time and then propels in a different direction with a different force, for another period of time and so on.
- The movement of the bacteria is very smooth, which indicates continuity of its position and velocity.
Given the random motion of bacteria, the outcome to such modelling will be the probability distribution of the model parameters and the time between changes of flagellar force.
|