Team:Michigan/Project/Modeling
From 2008.igem.org
|
|---|
|
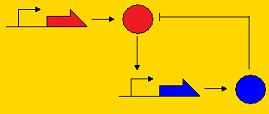
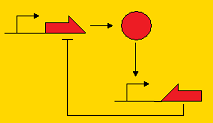
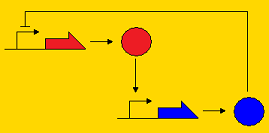
Sequestillator ModelingThe creation of a synthetic genetic clock has been considered by many people to be a "holy grail" of synthetic biology. Elowitz's "Repressilator" was one of the first synthetic clocks constructed, and it paved the way for consideration of other topologies that may promote oscillatory behavior, such as the Atkinson clock. A common characteristic of genetic clocks in general is the presence of a negative feedback loop (i.e. A activates B, and B represses A, so by repressing A, B indirectly its own concentration). In the Repressilator and the Atkinson clock, this repression occurred on the pre-transcriptional level; that is, the repressor protein prevented transcription of the activator gene. Below, we present three topologies of clocks with their modes of repression. Post-translational repression Pre-translational repression Pre-transcriptional repression
Note that the pre-transcriptional repression topology is the Atkinson clock without the positive feedback loop, and the post-translational clock is the Sequestillator. One of the goals of the modeling team is to understand the dynamics of this repression loop - i.e., how does the type of repression effect the robustness of the oscillator and the behavior (amplitude, periodicity, etc.). Analytically, it's pretty tough to answer these questions due to the multiple nonlinearities associated with the ODEs. However, numeric techniques can prove useful in helping answer our questions about robustness and behavior. We can pick lots of different, physiologically relevant parameter sets, put them into our ODEs, and see what trajectories we get. Particularly, going back to our question about robustness, we can assign a value for robustness. We define this value as the total number of parameter sets that give oscillatory behavior over all possible feasible parameter sets. Within our lab, we call this value the Ninfa index.
We created the "Indexilator" to calculate "relative" Ninfa indices (instead of dividing by the total feasible range of parameter space, divide by the number of trials you ran). The "Indexilator" is coded in Mathematica (we are currently working on programming a MatLab version). A commented copy of the code, followed by an example trial are given below. Anyone should free to utilize this code.
SEQUESTILLATOR MODELING PAGES These pages reference the different models that have been considered I couldn't include a lot of other simulations on the wiki because of some time constraints - but have no fear, for at iGEM they shall appear! We will have these simulations (and others) on our poster, so be sure to stop by to see our modeling! OTHER SIMULATIONS THAT WILL APPEAR AT iGEM 2008 (in less than two weeks!)
|
|---|
 "
"