|
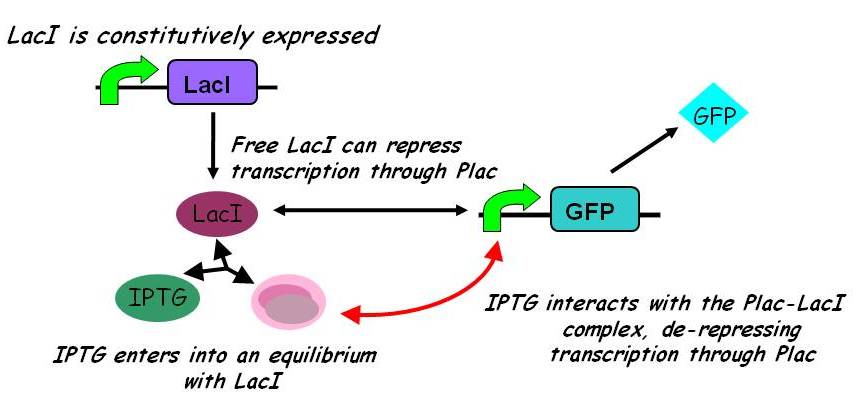
Equilibria
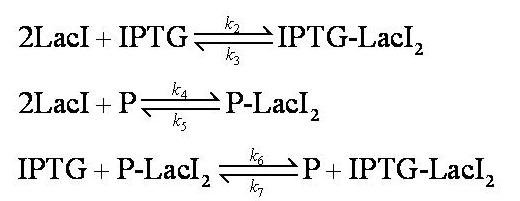
Assumptions:
No intermediary P-IPTG-LacI complex is formed.
We assumed 2 LacI molecules bind to the promoter, in accordance with the model description (2).
Note: k2, k3, k4, k5, k6 and k7 represent binding constants for formation and dissociation of complexes.
Equations
Before IPTG is introduced the system is in a steady state:

Note: k1 and k8 represent the rate of transcription through the constitutive promoter upstream of LacI and the promoter upstream of GFP respectively.
d1 and dGFP represent the degradation rates of LacI and GFP respectively.
kß is defined as k4/k5.
When IPTG is introduced, the dynamic behaviour of the system is described using a system of ODEs.
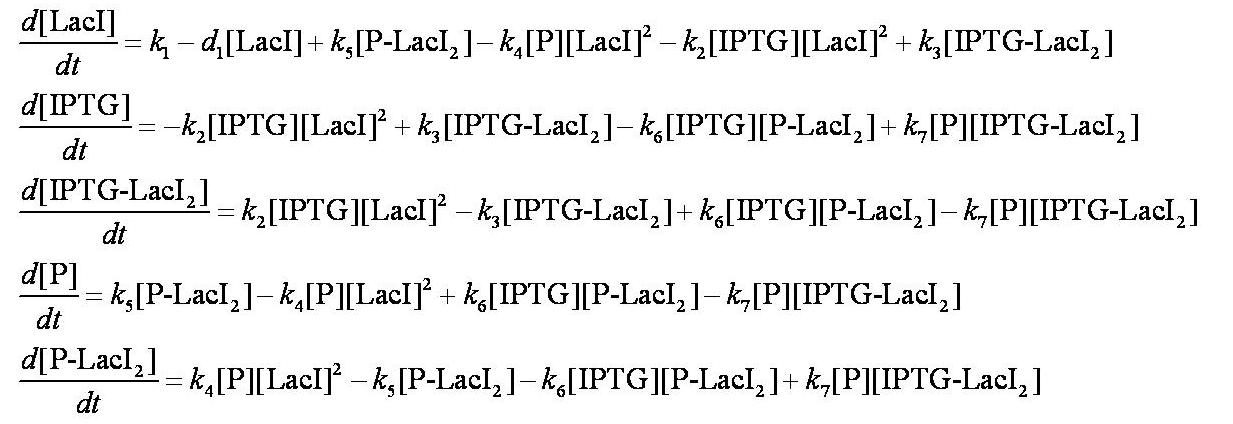
These are evaluated numerically using Matlab's ODE solver.
Qualitative effect of parameters on behaviour
Two different regimes of behaviour can be exhibited by the concentration of GFP over time as described by the more complex model, dependent on the parameters defining the ODE system.
Either the concentration of GFP increases up to a steady-state value, or it displays a hump, increasing to a maximum before returning to a lower steady-state level. This latter case is illustrated on the Genetic Circuit page but both cases can be explored using the simulations. The two regimes of behaviour are parameter-dependent and depend on the relative strengths of repression by LacI biding to the promoter and de-repression due to the interaction of IPTG with the Promoter-LacI complex.
It can be shown that the larger the ratio of relative strengths of de-repression and repression, the larger the gain in fluorescence before the steady state is reached.
|