|
Mathematical analysis and simulations
FIFO
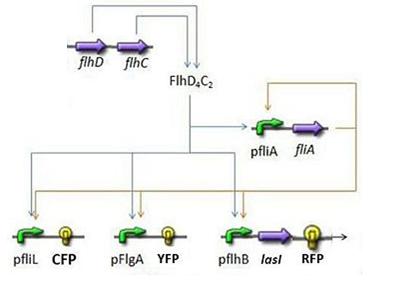
- In order to go further into the details of mathematical analysis of the FIFO, let us remind you the set of equations used and the corresponding network (note that you can have an explanation on the way they have been built on the Model Construction page):
where CFP, YFP, and RFP will be denoted below as respectively Z1,Z2 and Z3.
We have implemented this system using Matlab (see the corresponding codes)
- Then, in order to obtain simulations of the expected FIFO behaviour, we set ideal conditions, by imposing flhDC as a step function, equal to one then to zero.
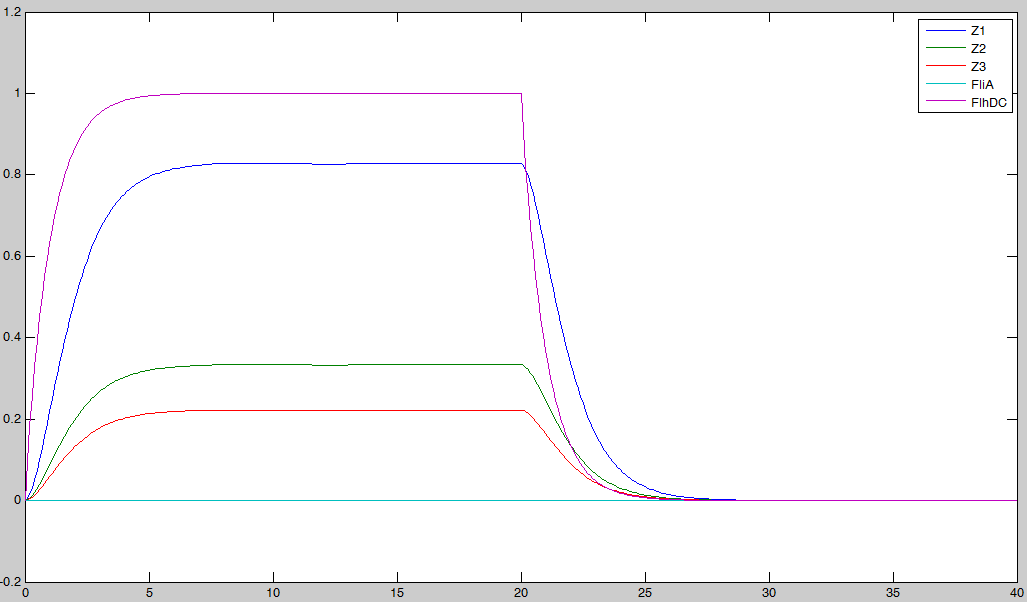
- We saw during the overall description of the core system that without FliA, the FIFO would presumably not work. We then simulated a first system, where [FliA] stays to zero value to confirm that qualitative conclusion :
Indeed, we may see that there is a LIFO behavior rather than the FIFO we expect...
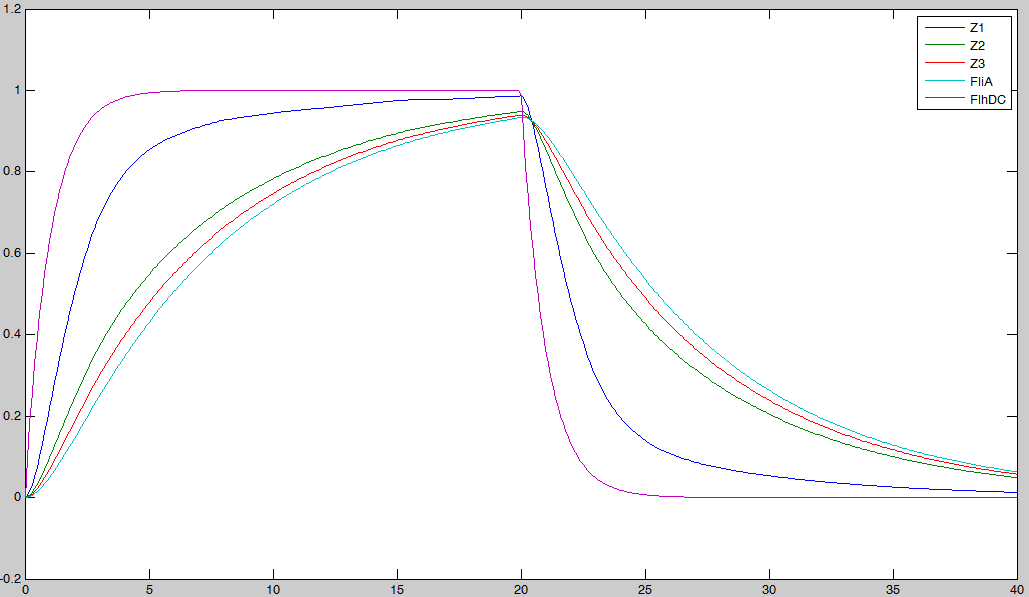
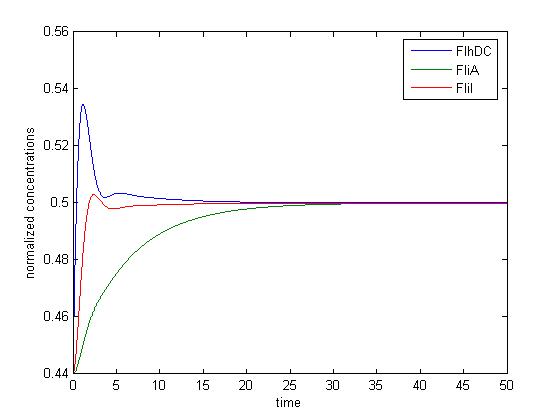
- Then, we simulated the entire system (that means with FliA), to check if we had
- the lasting burst due to FliA (more important for Z3 than for Z2, and more important for Z2 than Z1) in the increasing phase.
- the effect of fliA which maintained the concentrations to their maximum (more important for Z3 than for Z2, and more important for Z2 than Z1) in the decreasing phase. We have obtained the following curves, which are in perfect agreement with the theoretical definition of a 'FIFO' process :
- FliA enables the curves to cross, and adds a delay on the genes that are most affected, with gives a better observability of the FIFO behavior.
Oscillations
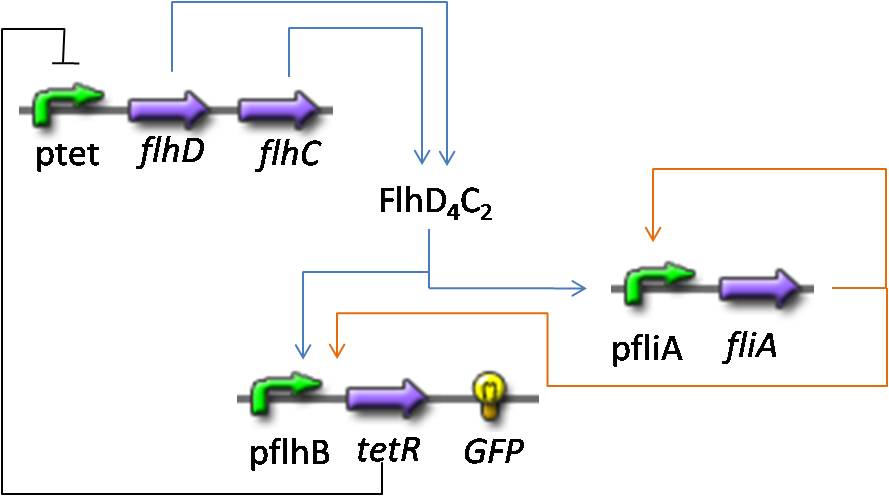
- In addition to the previous FIFO system, we will add a negative feedback on FlhDC promoter to observe oscillations. Thus, we obtained the following network and the corresponding equations :
If you want more details about the way we have built them, you can go to the model construction page.
If one tries to draw simulations of this system, he will obtain this kind of results :
In a nutshell : It does not work !
Nonetheless, there are two questions we could focus on:
Finally, the logical continuation of the process will be to try to improve the biological system in order to find oscillations. This will be described in the part below, as well as in the section System Improvements.
Parameters' changes
Since the core system has difficulties to produce oscillations, we brain-storm about possible modifications on the core system. We end up with two main possibilities :
- Try to change the parameters of the core system (see below).
- Try to device a novel system, based on the previous one (see the section System Improvements).
After testing our list of the possiblities , our main findings are:
| Description
| System
| Evaluation
| Observations
|
| Core system
|
| 
| Non oscillating system
|
| Removing the activation of envZ via FlhDC
| 
| 
| Modest damped oscillations
|
| Removing the auto-activation of flia
| 
|  
| Damped oscillations
|
| Removing both: the activation of envZ via FlhDC and the auto-activation of flia
| 
|  
| Damped oscillations with greater amplitud
|
| Enhancing the inhibition of FlhDC via envZ; Removing both: the activation of envZ via FlhDC and the auto-activation of flia
| 
|   
| Conserved oscillations
|
| Synchronized oscillations should be searched taking the last system as a starting point.
|
|
 "
"