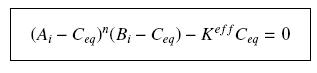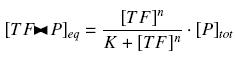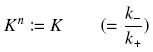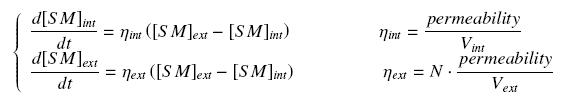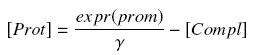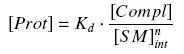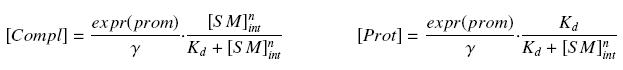Team:Paris/Modeling/Programs
From 2008.igem.org
(→Finding Parameters) |
|||
| (86 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | {{Paris/ | + | {{:Team:Paris/MenuBackup}} |
| - | == | + | ==Complexations Caracterisation== |
| - | + | ||
| - | + | The first hypothesis is that a complexation reaction is fully determined by the following : | |
| - | + | <center> [[Image:reacthill.jpg]] </center> | |
| - | + | and that the rates k<sub>+</sub> et k<sub>-</sub> stay constant under all conditions. Then, the second hypothesis is that these equations are (kinetically speaking) ''elementary'' : | |
| - | + | <center> [[Image:kinhill.jpg]] </center> | |
| + | and at steady-state : <center> [[Image:sshill.jpg]] </center> | ||
| - | + | Then, since we guess that the only datas we will have are the quantities of ''A'' and ''B'' introduced (''A<sub>i</sub>'' and ''B<sub>i</sub>''), the only equations we will deal with is the following, entirely determining the concentration ''C<sub>eq</sub>'' at steady-state (at least if we take the smallest real root of the equation, it is useless to demonstrate the unicity, or even the existence, of such a solution) : | |
| - | + | ||
| - | + | ||
| - | + | <center> [[Image:Eqnss.jpg]] </center> | |
| - | [[Image: | + | ==Equilibrium of a Complex== |
| + | |||
| + | Know, if we imagine a given amount of ''A<sub>i</sub>'' and ''B<sub>i</sub>'', that are calculated as their equilibrium without taking acount of their complexation (but, for instance, of other interactions, productions and disappearance), and that the produced complex C disappears along time with a ''degradation rate γ'', we get : | ||
| + | |||
| + | [[Image:GammaC.jpg|center]] | ||
| + | |||
| + | so that the equilibrium gives : | ||
| + | |||
| + | [[Image:EqGammaC.jpg|center]] | ||
| + | |||
| + | with | ||
| + | |||
| + | [[Image:Keff.jpg|center]] | ||
| + | |||
| + | ==Hill Functions== | ||
| + | |||
| + | The previous system of complexation applied in particular to the association of the Promoters (''P'') and its Transcription Factor (''TF''). | ||
| + | |||
| + | Because the promoters on a "low copy plasmid" exists in the cell in ten exemplaries, in contrary to a protein, which, as long as it is produced (even weakly) exists in thousands of exemplaries, we assume can the quantities of ''TF'' and ''P'' are different by several orders of magnitude. Then, with the previous notations, if ''A'', ''B'' and ''C'' stands respectively for ''TF'', ''P'' and the complex ''TF><P'', we will get | ||
| + | |||
| + | [[Image:approxhill.jpg|center]] | ||
| + | |||
| + | that we can easily solve with : | ||
| + | |||
| + | [[Image:reshill.jpg|center]] | ||
| + | |||
| + | Depending to the order ''' ''n'' ''' (also called ''cooperativity'', because it correponds to the possibilities of the transcription factor to binds in a group on the promoter), this function is a ''sigmoïd'', known as the ''Hill function''. The parameter ''' ''K'' ''', called ''activation constant'', is often replaced in the previous expression by the following notation | ||
| + | |||
| + | [[Image:changeK.jpg|center]] | ||
| + | |||
| + | It simplifies the manipulations of the expression ; we can notice that ''' ''K'' ''' represents now the amount of ''TF'' needed to bind half of the total ''P'' in the cell. | ||
| + | |||
| + | [[Image:hilldef.jpg|center]] | ||
| + | |||
| + | ==Induction by a small molecule== | ||
| + | |||
| + | ===Introduction=== | ||
| + | In certain steps of our [[Team:Paris/Project|system]], and in our [[Team:Paris/Modeling/estimation|caracterisation plan]], we use the diffusion of a small molecule (''SM''), that binds to a transcription factor. | ||
| + | |||
| + | We make the hypothesis of a '''simple, passive diffusion''', that leads at the steady-state at equal amount of the small molecule, inside and outside the cells. The resulting equations are the following coupling : | ||
| + | |||
| + | [[Image:CouplDiff.jpg|center]] | ||
| + | |||
| + | where | ||
| + | |||
| + | * ''permeability'' is the membrane permeability multiplied by the average external surface of a cell (in min<sup>-1</sup>) | ||
| + | * ''N'' is the average cell population | ||
| + | * ''V<sub>int</sub>'' is the average volume of a cell (in L) ; ''V<sub>ext</sub>'' is the volume of the culture medium outer the cells (in L) | ||
| + | |||
| + | ===The situation=== | ||
| + | |||
| + | The involvement of the previous process is, in our systems,under these conditions : | ||
| + | |||
| + | * ''Prot'' is a protein, produce by a ''promoter'' | ||
| + | * ''expr_prom'' is the given expression of this ''promoter'' (production rate of ''Prot'') | ||
| + | * ''γ'' is the degradation/dilution rate of the proteins and complexes in the cell (especially due to cell division, we made so far the hypothesis that it is the same for all the proteins) | ||
| + | * ''SM<sub>int</sub>'' binds to ''Prot'', with a cooperativity ''n'' and a dissociation constant ''K<sub>d</sub>'', to form the complex ''Compl'' | ||
| + | * The cell culture is in a chemostat : the cell population is N; The renewal rate (flow of the medium, divided by the volume of the chemostat, in min<sup>-1</sup>) is ''rnw''; The Volume of a cell is ''V<sub>int</sub>''; and of the outer medium is ''V<sub>ext</sub>'' ( = ''Volume(chemostat)'' - ''N'' * ''V<sub>int</sub>'') | ||
| + | |||
| + | ===Induction for the caracterisations=== | ||
| + | see [[Team:Paris/Modeling/estimation#How_to_control_the_concentration_of_the_transcription_factor_.3F| details on the induction]] | ||
| + | |||
| + | In these experimental conditions, we assume that the external concentration of SM remains constant. So, at steady-state, | ||
| + | <center>[''SM'']<sub>ext</sub> = [''SM'']<sub>int</sub></center> | ||
| + | |||
| + | Then, considering the previous complexations equations, and by the equilibrium of ''Prot'' ( ''expr(prom)'' denotes protein production rate ), we have at steady states | ||
| + | |||
| + | [[Image:ProtSt.jpg|center]] | ||
| + | |||
| + | and by the definition of the dissociation constant | ||
| + | |||
| + | [[Image:Kd.jpg|center]] | ||
| + | |||
| + | that leads to the following expression of the complexes and proteins : | ||
| + | |||
| + | [[Image:ComplProt.jpg|center]] | ||
| + | |||
| + | These equations will be used to estimate ''K<sub>d</sub>'' and ''n'', and then to estimate the relative amount of bound or free protein in the cell, for a given amount of ''SM''. | ||
| + | |||
| + | |||
| + | |||
| + | ==Finding Parameters== | ||
| - | + | |}<br style="clear:both" /> | |
Latest revision as of 07:06, 30 October 2008
Go back to the normal Wiki
Contents |
Complexations Caracterisation
The first hypothesis is that a complexation reaction is fully determined by the following :
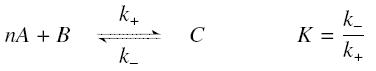
and that the rates k+ et k- stay constant under all conditions. Then, the second hypothesis is that these equations are (kinetically speaking) elementary :
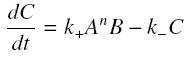
Then, since we guess that the only datas we will have are the quantities of A and B introduced (Ai and Bi), the only equations we will deal with is the following, entirely determining the concentration Ceq at steady-state (at least if we take the smallest real root of the equation, it is useless to demonstrate the unicity, or even the existence, of such a solution) :
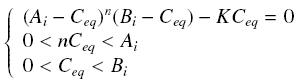
Equilibrium of a Complex
Know, if we imagine a given amount of Ai and Bi, that are calculated as their equilibrium without taking acount of their complexation (but, for instance, of other interactions, productions and disappearance), and that the produced complex C disappears along time with a degradation rate γ, we get :
so that the equilibrium gives :
with
Hill Functions
The previous system of complexation applied in particular to the association of the Promoters (P) and its Transcription Factor (TF).
Because the promoters on a "low copy plasmid" exists in the cell in ten exemplaries, in contrary to a protein, which, as long as it is produced (even weakly) exists in thousands of exemplaries, we assume can the quantities of TF and P are different by several orders of magnitude. Then, with the previous notations, if A, B and C stands respectively for TF, P and the complex TF><P, we will get
that we can easily solve with :
Depending to the order n (also called cooperativity, because it correponds to the possibilities of the transcription factor to binds in a group on the promoter), this function is a sigmoïd, known as the Hill function. The parameter K , called activation constant, is often replaced in the previous expression by the following notation
It simplifies the manipulations of the expression ; we can notice that K represents now the amount of TF needed to bind half of the total P in the cell.
Induction by a small molecule
Introduction
In certain steps of our system, and in our caracterisation plan, we use the diffusion of a small molecule (SM), that binds to a transcription factor.
We make the hypothesis of a simple, passive diffusion, that leads at the steady-state at equal amount of the small molecule, inside and outside the cells. The resulting equations are the following coupling :
where
- permeability is the membrane permeability multiplied by the average external surface of a cell (in min-1)
- N is the average cell population
- Vint is the average volume of a cell (in L) ; Vext is the volume of the culture medium outer the cells (in L)
The situation
The involvement of the previous process is, in our systems,under these conditions :
- Prot is a protein, produce by a promoter
- expr_prom is the given expression of this promoter (production rate of Prot)
- γ is the degradation/dilution rate of the proteins and complexes in the cell (especially due to cell division, we made so far the hypothesis that it is the same for all the proteins)
- SMint binds to Prot, with a cooperativity n and a dissociation constant Kd, to form the complex Compl
- The cell culture is in a chemostat : the cell population is N; The renewal rate (flow of the medium, divided by the volume of the chemostat, in min-1) is rnw; The Volume of a cell is Vint; and of the outer medium is Vext ( = Volume(chemostat) - N * Vint)
Induction for the caracterisations
In these experimental conditions, we assume that the external concentration of SM remains constant. So, at steady-state,
Then, considering the previous complexations equations, and by the equilibrium of Prot ( expr(prom) denotes protein production rate ), we have at steady states
and by the definition of the dissociation constant
that leads to the following expression of the complexes and proteins :
These equations will be used to estimate Kd and n, and then to estimate the relative amount of bound or free protein in the cell, for a given amount of SM.
Finding Parameters
|}
 "
"