Team:Purdue/Modeling
From 2008.igem.org
(Difference between revisions)
| Line 41: | Line 41: | ||
|[[Image:PurdueIntersectionsModel.jpg|10px|center|frame]] | |[[Image:PurdueIntersectionsModel.jpg|10px|center|frame]] | ||
| - | |- | + | |-|} |
| Line 50: | Line 50: | ||
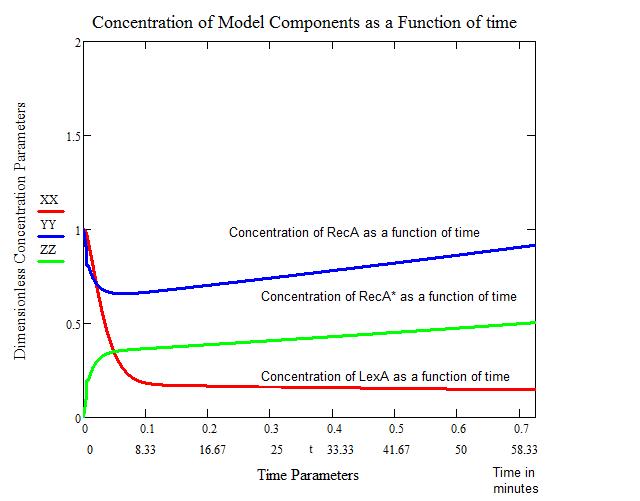
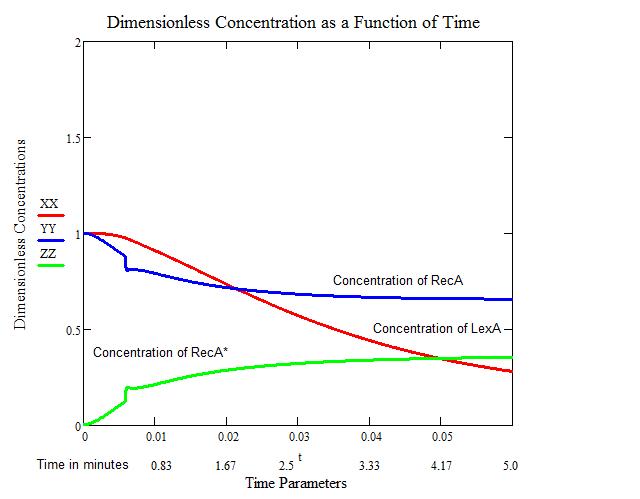
''All Calculations and the figures above were performed in MathCad, utilizing built in Runge-Kutta 4th order function, by Craig Barcus, utilizing the mathematical model presented by SV. Aksenov in 1997.'' | ''All Calculations and the figures above were performed in MathCad, utilizing built in Runge-Kutta 4th order function, by Craig Barcus, utilizing the mathematical model presented by SV. Aksenov in 1997.'' | ||
| - | + | ||
<!--- The Mission, Experiments ---> | <!--- The Mission, Experiments ---> | ||
Revision as of 16:47, 25 September 2008
Modeling Objectives
- Develop a mechanistics ODE model of the population to predict gene expression dynamics
- Question? .... Will the color production be fast enough to be useful to the user? Or will it be too late?
- What is the relationship between UV exposure and reporter gene expression?
- Can we construct a useful calibration curve of color as a function of UV?
Modeling References
- 1997. "Mathematical model of the SOS response regulation of an excision repair deficient mutant of Escherichia coli after UV light irradation". [1]. Off-the-shelf mechanistic model of the SOS response. Utilized as the basic model for our system.
- 2005. "Response times and mechanisms of SOS induction by attaching promoters to GFP: "Precise Temporal Modulation in the Response of the SOS DNA Repair Network in Individual Bacteria" [2]. Potential Validation Data Set. Model should predict similar dynamics.
Modeling the SOS response in a uvr- mutant (No nucleotide excision repair)
Assumptions
- The UV light intensity is constant and instantaneous.
- The bacteria are not undergoing any type of DNA repair at the time of UV exposure.
- Thymine dimer formation is the major DNA damage occurring.
| Home | The Team | The Project | Parts Submitted to the Registry | Modeling | Notebook | Tools and References |
|---|
 "
"